Cho hàm số y = - x^2 có đồ thị là Parabol ( P ). a) Vẽ đồ thị ( P ) của hàm số đã cho. b) Tìm tọa

Câu hỏi
Nhận biếtCho hàm số \(y = - {x^2}\) có đồ thị là Parabol \(\left( P \right)\).
a) Vẽ đồ thị \(\left( P \right)\) của hàm số đã cho.
b) Tìm tọa độ giao điểm của \(\left( P \right)\) và đường thẳng \(\left( d \right):{\mkern 1mu} {\mkern 1mu} y = - 2x + 1\) bằng phép tính.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a) Ta có bảng giá trị sau:

Vẽ đồ thị \(\left( P \right)\) ở hình vẽ bên.
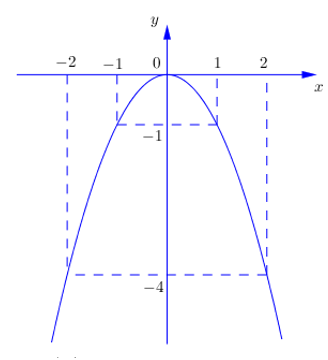
b) Xét phương trình hoành độ giao điểm của đồ thị hàm số \(\left( P \right)\) và đường thẳng \(\left( d \right)\) là:
\(\begin{array}{l} - {x^2} = - 2x + 1 \Leftrightarrow {\left( {x - 1} \right)^2} = 0 \Leftrightarrow x = 1\\ \Rightarrow y = - {1^2} = - 1.\end{array}\).
Vậy giao điểm của \(\left( P \right)\) và đường thẳng \(\left( d \right)\) là điểm \(A\left( {1; - 1} \right)\).
Chọn A

