Cho hàm số y = 2x^2 có đồ thị là ( P ). a) Vẽ đồ thị ( P ). b) Tìm tham số m để đường thẳng ( d ):

Câu hỏi
Nhận biếtCho hàm số \(y = 2{x^2}\) có đồ thị là \(\left( P \right).\)
a) Vẽ đồ thị \(\left( P \right).\)
b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):\,\,\,y = mx - 2\) tiếp xúc với \(\left( P \right).\)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a) Vẽ đồ thị \(\left( P \right).\)
Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( P \right):\,\,\,y = 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2;\,\,8} \right),\,\,\left( { - 1;\,2} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\,\,2} \right),\,\,\left( {2;\,\,8} \right)\) và nhận trục \(Oy\) làm trục đối xứng.
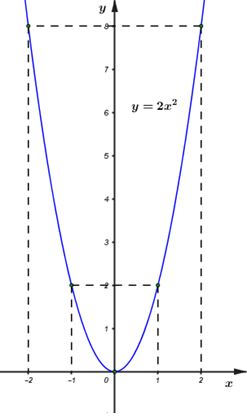
b) Tìm tham số \(m\) để đường thẳng \(\left( d \right):\,\,\,y = mx - 2\) tiếp xúc với \(\left( P \right).\)
Phương trình hoành độ giao điểm của hai đồ thị hàm số là: \(2{x^2} = mx - 2 \Leftrightarrow 2{x^2} - mx + 2 = 0\,\,\,\left( * \right)\)
Đường thẳng \(d\) tiếp xúc với parabol \(\left( P \right) \Leftrightarrow \,\,\left( * \right)\) có nghiệm kép
\( \Leftrightarrow \Delta = 0 \Leftrightarrow {m^2} - 4.2.2 = 0 \Leftrightarrow {m^2} = 16 \Leftrightarrow \left[ \begin{array}{l}m = 4\\m = - 4\end{array} \right..\)
Vậy với \(m = 4\) hoặc \(m = - 4\) thì thỏa mãn bài toán.
Chọn D.

