Cho hàm số y = 2x^2 - 4x - 1 có đồ thị như hình vẽ bên dưới:
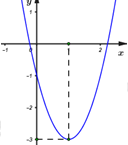
Câu hỏi
Nhận biếtCho hàm số \(y = 2{x^2} - 4x - 1\) có đồ thị như hình vẽ bên dưới:
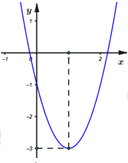
Phương trình \(\left| {2{x^2} - 4x - 1} \right| = m\) (với \(m\) là tham số) có hai nghiệm khi và chỉ khi \(m\) thuộc tập hợp nào sau đây?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
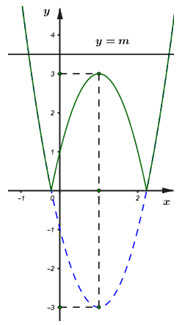
Vẽ đồ thị \(y = \left| {2{x^2} - 4x - 1} \right|\) bằng cách:
Giữ nguyên phần nằm trên \(Ox\) của đồ thị hàm số \(y = 2{x^2} - 4x - 1\);
Lấy đối xứng phần nằm dưới \(Ox\) qua \(Ox.\)
Xóa bỏ phần nằm dưới \(Ox.\)
Ta có đồ thị hàm số như hình vẽ bên.
Nghiệm của \(\left| {2{x^2} - 4x - 1} \right| = m\) là giao của 2 đồ thị hàm số \(y = \left| {2{x^2} - 4x - 1} \right|\)
và \(y = m\) với \(y = m\) là đường thẳng song song \(Ox.\)
Khi đó để phương trình có 2 nghiệm thì \(\left[ \begin{array}{l}m = 0\\m > 3\end{array} \right.\)
Chọn B.

