Cho hàm số y = 2x – 3 có đồ thị là ( d1 ) và hàm số y=x2 có đồ thị l

Câu hỏi
Nhận biếtCho hàm số \(y = 2x – 3\) có đồ thị là \(\left( {{d}_{1}} \right)\) và hàm số \(y=\frac{x}{2}\) có đồ thị là \(\left( {{d}_{2}} \right)\).
a) Vẽ \(\left( {{d}_{1}} \right)\) và \(\left( {{d}_{2}} \right)\) trên cùng mặt phẳng tọa độ.
b) Tìm các giá trị của m để đường thẳng \(({{d}_{3}}):y=-3x+m-2\) cắt đường thẳng\(\left( {{d}_{1}} \right)\) tại điểm M
có tung độ bằng – 1.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Giải:
a) Bảng giá trị:

Vẽ (d1) và (d2) trên cùng mặt phẳng Oxy
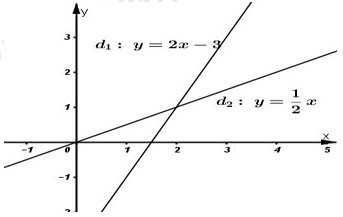
b)
b) Theo đề bài ta có: \(M\left( {{x}_{0}};-1 \right);\,\,\,M\in {{d}_{1}}\Rightarrow -1=2{{x}_{0}}-3\Leftrightarrow {{x}_{0}}=1\Rightarrow M\left( 1;-1 \right).\)
Lại có \(M\in {{d}_{3}}\Rightarrow -3.1+m-2=-1\Leftrightarrow m=4.\)
Vậy \(m=4.\)

