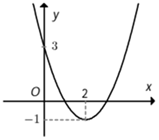
Cho hàm số f( x ) = ax^2 + bx + c có đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số

Câu hỏi
Nhận biếtCho hàm số \(f\left( x \right) = a{x^2} + bx + c\) có đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số \(m\)thì phương trình \(\left| {f\left( x \right)} \right| - 1 = m\) có đúng 2 nghiệm phân biệt?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
+) Phương trình \(\left| {f\left( x \right)} \right| - 1 = m \Leftrightarrow \left| {f\left( x \right)} \right| = m + 1.\)
+) Đồ thị của hàm số \(y = \left| {f\left( x \right)} \right|\) là:
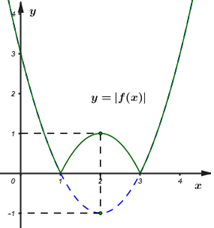
Dựa vào đồ thị, để phương trình \(\left| {f\left( x \right)} \right| = m + 1\) có hai nghiệm phân biệt \( \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m + 1 > 1}\\{m + 1 = 0}\end{array} \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{m > 0}\\{m = - 1}\end{array}} \right.} \right.\)
Chọn C