Cho hàm số bậc nhất y = ( m + 1 )x + 2 có đồ thị ( d ) (m là tham số và m ne - 1) a) Vẽ ( d ) khi

Câu hỏi
Nhận biếtCho hàm số bậc nhất \(y = \left( {m + 1} \right)x + 2\) có đồ thị \(\left( d \right)\) (\(m\) là tham số và \(m \ne - 1\))
a) Vẽ \(\left( d \right)\) khi \(m = 0\).
b) Xác định \(m\) để đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 1\).
c) Xác định \(m\) để \(\left( d \right)\) cắt hai trục \(Ox,Oy\) tại \(A\) và \(B\) sao cho tam giác \(AOB\) có diện tích bằng \(2\) (đơn vị diện tích).
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
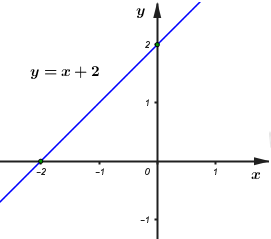
a) Khi \(m = 0\) ta có \(\left( d \right):\,y = x + 2\)
Với \(x = 0 \Rightarrow y = 2\)
\(x = - 2 \Rightarrow y = 0\)
Đồ thị hàm số \(y = x + 2\) là đường thẳng \(\left( d \right)\) đi qua hai điểm có tọa độ \(\left( {0;2} \right),\left( { - 2;0} \right)\).
Hình vẽ:
b) Xác định \(m\) để đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 1\).
Đường thẳng \(\left( d \right)\) song song với đường thẳng \(y = 2x + 1\)
\( \Leftrightarrow \left\{ \begin{array}{l}m + 1 = 2\\2 \ne 1\end{array} \right. \Leftrightarrow m = 1\)
Kết hợp điều kiện \(m \ne - 1\) ta có \(m = 1\,\,\left( {tm} \right).\)
Vậy \(m = 1\).
c) Xác định \(m\) để \(\left( d \right)\) cắt hai trục \(Ox,Oy\) tại \(A\) và \(B\) sao cho tam giác \(AOB\) có diện tích bằng \(2\) (đơn vị diện tích)
Do \(m \ne - 1\) nên không mất tính tổng quát ta giả sử \(\left( d \right)\) cắt \(Ox\) và \(Oy\) như hình vẽ
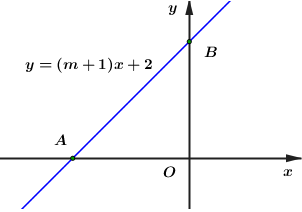
Vì \(A\) là giao điểm của \(\left( d \right)\) với \(Ox\) nên \(A\left( {x;0} \right) \Rightarrow \left( {m + 1} \right)x + 2 = 0 \Rightarrow x = - \frac{2}{{m + 1}}\)
Suy ra \(A\left( { - \frac{2}{{m + 1}};0} \right) \Rightarrow OA = \frac{2}{{\left| {m + 1} \right|}}\)
Vì \(B\) là giao điểm của \(\left( d \right)\) với \(Oy\) nên \(B\left( {0;y} \right) \Rightarrow \left( {m + 1} \right).0 + 2 = y \Rightarrow y = 2\)
Suy ra \(B\left( {0;2} \right) \Rightarrow OB = 2\)
Vì \(\Delta OAB\) vuông tại \(O\).
Khi đó: \({S_{\Delta OAB}} = \frac{1}{2}.OA.OB = \frac{1}{2}.\frac{2}{{\left| {m + 1} \right|}}.2 = \frac{2}{{\left| {m + 1} \right|}}\)
Mà \({S_{\Delta OAB}} = 2 \Leftrightarrow \left| {m + 1} \right| = 1\) \( \Leftrightarrow \left[ \begin{array}{l}m + 1 = 1\\m + 1 = - 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = - 2\end{array} \right.\) (thỏa mãn \(m \ne - 1\))
Vạy \(m = 0\) hoặc \(m = - 2\) thỏa mãn yêu cầu bài toán.
Chọn B.

