Cho hàm số bậc nhất y=( 2m-1 )x+3 có đồ thị là đường thẳng ( d ). a) Vẽ đồ thị hàm số m=32. b) Tì

Câu hỏi
Nhận biếtCho hàm số bậc nhất \(y=\left( 2m-1 \right)x+3\) có đồ thị là đường thẳng \(\left( d \right).\)
a) Vẽ đồ thị hàm số \(m=\frac{3}{2}.\)
b) Tìm \(m\) để đường thẳng \(\left( d \right)\) và hai đường thẳng \(y=x+3\) và \(y=2x+1\) đồng quy?
c) Gọi hai điểm \(A\) và \(B\) là giao điểm của \(\left( d \right)\) với lần lượt hai trục \(Ox,\ Oy.\) Tìm \(m\) để diện tích tam giác \(OAB\) bằng \(3\) (đvdt)?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
a) Vẽ đồ thị hàm số \(m=\frac{3}{2}.\)
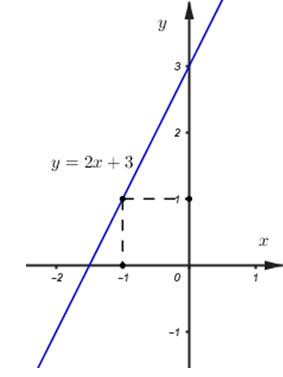
Với \(m=\frac{3}{2}\) ta có: \(\left( d \right):\ y=2x+3.\)
Ta có bảng giá trị:

Đồ thị của đường thẳng \(\left( d \right)\) đi qua hai điểm \(\left( 0;\ 3 \right)\) và \(\left( -1;\ 1 \right).\)
b) Tìm \(m\) để đường thẳng \(\left( d \right)\) và hai đường thẳng \(y=x+3\) và \(y=2x+1\) đồng quy?
Tọa độ giao điểm của hai đường thẳng \(y=x+3\) và \(y=2x+1\) là nghiệm của hệ phương trình:
\(\left\{ \begin{array}{l}
y = x + 3\\
y = 2x + 1
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x - 2 = 0\\
y = x + 3
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
x = 2\\
y = 5
\end{array} \right. \Rightarrow A\left( {2;\;5} \right).\)
Đường thẳng \(\left( d \right)\) và hai đường thẳng \(y=x+3,\ \ y=2x+1\) đồng quy \(\Leftrightarrow A\left( 2;\ 5 \right)\in \left( d \right).\)
\(\Rightarrow 5=\left( 2m-1 \right).2+3\Leftrightarrow 2\left( 2m-1 \right)=2\Leftrightarrow 2m-1=1\Leftrightarrow m=1.\)
Vậy \(m=1\) thỏa mãn bài toán.
c) Gọi hai điểm \(A\) và \(B\) là giao điểm của \(\left( d \right)\) với lần lượt hai trục \(Ox,\ Oy.\) Tìm \(m\) để diện tích tam giác \(OAB\) bằng \(3\) (đvdt)?
Hàm số đã cho là hàm số bậc nhất nên \(2m-1\ne 0\Leftrightarrow m\ne \frac{1}{2}.\)
Gọi hai điểm \(A\) và \(B\) là giao điểm của \(\left( d \right)\) với lần lượt hai trục \(Ox,\ Oy.\)
\(\Rightarrow A\left( -\frac{3}{2m-1};\ 0 \right),\ \ B\left( 0;\ 3 \right)\)
Khi đó ta có \(\Delta OAB\) vuông tại \(O.\)
\(\begin{array}{l}
\Rightarrow {S_{OAB}} = \frac{1}{2}OA.OB = \frac{1}{2}.\left| {{x_A}} \right|.\left| {{y_B}} \right| = 3\\
\Leftrightarrow \frac{1}{2}.\left| { - \frac{3}{{2m - 1}}} \right|.3 = 3 \Leftrightarrow \frac{3}{{\left| {2m - 1} \right|}} = 2\\
\Leftrightarrow \left| {2m - 1} \right| = \frac{3}{2} \Leftrightarrow \left[ \begin{array}{l}
2m - 1 = \frac{3}{2}\\
2m - 1 = - \frac{3}{2}
\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}
m = \frac{5}{4}\;\;\left( {tm} \right)\\
m = -\frac{1}{4}\;\;\left( {tm} \right)
\end{array} \right..
\end{array}\)
Vậy \(m=\frac{5}{4},\ \ m=-\frac{1}{4}\) thỏa mãn điều kiện bài toán.
Chọn B

