Cho hai lực F1 và F2 cùng có điểm đặt là O. Cường độ của F1 là 60N góc giữa F1 và F2 bằng

Câu hỏi
Nhận biếtCho hai lực \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) cùng có điểm đặt là O. Cường độ của \(\overrightarrow {{F_1}}\) là 60N góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng 900. Cường độ lực tổng hợp của \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) là 100N. Cường độ của \(\overrightarrow {{F_2}} \)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta có tổng hợp lực của \(\overrightarrow {{F_1}} ,\overrightarrow {{F_2}} \) được xác định như hình vẽ.
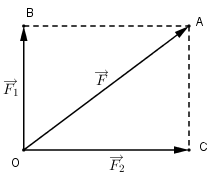
Vì góc giữa \(\overrightarrow {{F_1}} \) và \(\overrightarrow {{F_2}} \) bằng \({90^0}\) nên \(\Delta OAC\) vuông tại C.
Ta có: \(OA = \left| {\overrightarrow F } \right| = 100,AC = \left| {\overrightarrow {{F_1}} } \right| = 60\)
Áp dụng định lí Pi – ta – go ta có: \(AC = \sqrt {O{A^2} - O{C^2}} = \sqrt {{{100}^2} - {{60}^2}} = 80.\)
\( \Rightarrow \overrightarrow {{F_2}} = 80N.\)
