Cho hai hàm số y = 2x^2 và y = - 2x + 4. a) Vẽ đồ thị các hàm số này

Câu hỏi
Nhận biếtCho hai hàm số \(y = 2{x^2} \) và \(y = - 2x + 4 \).
a) Vẽ đồ thị các hàm số này trên cùng một phẳng tọa độ.
b) Tìm tọa độ hai giao điểm A và B của hai đồ thị đó. Tính khoảng cách từ điểm \(M \left( { - 2;0} \right) \) đến đường thẳng \(AB \).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a) Vẽ đồ thị các hàm số này trên cùng một phẳng tọa độ.
Ta có bảng giá trị của hàm số \(y = 2{x^2}\)

Vẽ đường cong đi qua các điểm có tọa độ \(\left( { - 2;8} \right),\left( { - 1;2} \right),\left( {0;0} \right),\left( {1;2} \right),\left( {2;8} \right)\) ta được parabol \(\left( P \right):y = 2{x^2}\)
Bảng giá trị của hàm số \(y = - 2x + 4\)
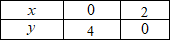
Vẽ đường thẳng đi qua hai điểm có tọa độ \(\left( {0;4} \right),\left( {2;0} \right)\) ta được đường thẳng \(d:y = - 2x + 4\)
Đồ thị hàm số:
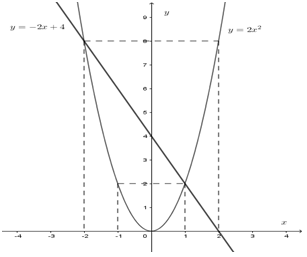
b) Tìm tọa độ hai giao điểm A và B của hai đồ thị đó. Tính khoảng cách từ điểm \(M\left( { - 2;0} \right)\) đến đường thẳng \(AB\).
Xét phương trình hoành độ giao điểm của đường thẳng \(d:y = - 2x + 4\) và parabol \(\left( P \right):y = 2{x^2}\)
\(\begin{array}{l}\,\,\,\,\,\,\,2{x^2} = - 2x + 4 \Leftrightarrow 2{x^2} + 2x - 4 = 0\\ \Leftrightarrow {x^2} + x - 2 = 0 \Leftrightarrow {x^2} - x + 2x - 2 = 0\\ \Leftrightarrow x\left( {x - 1} \right) + 2\left( {x - 1} \right) = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 1 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = 1 \Rightarrow y = {2.1^2} = 2\\x = - 2 \Rightarrow y = 2.{\left( { - 2} \right)^2} = 8\end{array} \right.\end{array}\)
Vậy giao điểm của \(\left( P \right)\) và \(\left( d \right)\) là \(A\left( {1;2} \right),\,\,B\left( { - 2;8} \right)\).
* Tính khoảng cách từ \(M\left( { - 2;0} \right)\) đến đường thẳng \(AB.\)
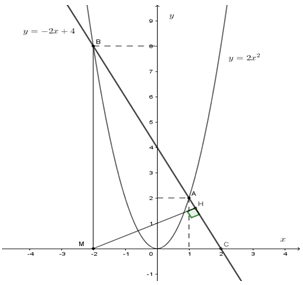
Kẻ \(MH \bot AB\,\,\left( {M \in AB} \right)\). Nhận xét thấy khoảng cách từ \(M\left( { - 2;0} \right)\) xuống đường thẳng \(AB\) chính là \(MH\).
Gọi \(C = d \cap Ox \Rightarrow C\left( {2;0} \right)\)
Lại thấy \(B\left( { - 2;8} \right);M\left( { - 2;0} \right) \Rightarrow \) Phương trình đường thẳng \(BM\) là \(x = - 2 \Rightarrow BM \bot Ox\) hay \(BM \bot MC\) suy ra tam giác \(BMC\) vuông tại \(M\).
Ta lại có \(B\left( { - 2;8} \right);\,\,M\left( { - 2;0} \right);\,\,C\left( {2;0} \right) \Rightarrow BM = 8;\,\,CM = 4\)
Xét tam giác \(BMC\) vuông tại \(M\) có \(MH\) là đường cao nên
\(\frac{1}{{M{H^2}}} = \frac{1}{{B{M^2}}} + \frac{1}{{M{C^2}}} = \frac{1}{{{8^2}}} + \frac{1}{{{4^2}}} = \frac{5}{{64}} \Leftrightarrow MH = \frac{{8\sqrt 5 }}{5}\)
Vậy khoảng cách cần tìm là \(MH = \frac{{8\sqrt 5 }}{5}.\)
Chọn A.

