Cho hai hàm số (P): , y=x^2 và đường thẳng d: , y = x + 6. a) Xác đ

Câu hỏi
Nhận biếtCho hai hàm số \( (P): \, y=x^2 \) và đường thẳng \(d: \, y = x + 6 \).
a) Xác định tọa độ giao điểm A và B của đường thẳng d và parabol (P).
b) Tính diện tích tam giác AOB với O là gốc tọa độ.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a) Phương trình hoành độ giao điểm của đồ thị hàm số (P) và đường thẳng d là:
\( \eqalign{ & \,\,\,\,\,\,\,\,{x^2} = x + 6 \cr & \Leftrightarrow {x^2} - x - 6 = 0 \cr & \Leftrightarrow {x^2} - 3x + 2x - 6 = 0 \cr & \Leftrightarrow \left( {x - 3} \right)\left( {x + 2} \right) = 0 \cr & \Leftrightarrow \left[ \matrix{ x - 3 = 0 \hfill \cr x + 2 = 0 \hfill \cr} \right. \Leftrightarrow \left[ \matrix{ x = 3 \hfill \cr x = - 2 \hfill \cr} \right. \cr} \)
+) Với \( x = 3\) ta có: \( y = 3 + 6 = 9 \Rightarrow A\left( {3;9} \right). \)
+) Với \( x = – 2\) ta có: \( y = –2 + 6 = 4 \Rightarrow B\left( { - 2;4} \right)\).
b) Ta có đồ thị hai hàm số như hình vẽ:
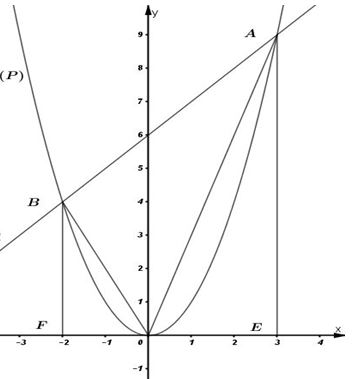
Ta có: \({S_{AOB}} = {S_{ABFE}} - {S_{BFO}} - {S_{AOE}}. \)
\(\eqalign{ & + )\,\,{S_{ABFE}} = {1 \over 2}\left( {BF + AE} \right).EF = {1 \over 2}\left( {4 + 9} \right).5 = {{65} \over 2}. \cr & + )\,\,{S_{BFO}} = {1 \over 2}BF.OF = {1 \over 2}.4.2 = 4. \cr & + )\,\,{S_{AOE}} = {1 \over 2}OE.AO = {1 \over 2}.3.9 = {{27} \over 2}. \cr & \Rightarrow {S_{AOB}} = {S_{ABFE}} - {S_{BFO}} - {S_{AOE}} = {{65} \over 2} - 4 - {{27} \over 2} = 15. \cr} \)
Vậy diện tích tam giác AOB là 15 đvdt.
Chọn A.

