Cho hai đường thẳng ( d1 ):2x + 3y - 5 = 0;( d2 ):x + y - 2 = 0. Lập p

Câu hỏi
Nhận biếtCho hai đường thẳng \(\left( {{d_1}} \right):\,\,2x + 3y - 5 = 0;\,\,\left( {{d_2}} \right):\,\,x + y - 2 = 0\). Lập phương trình đường thẳng \(\left( {{d_3}} \right)\) đối xứng với \(\left( {{d_1}} \right)\) qua \(\left( {{d_2}} \right)\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
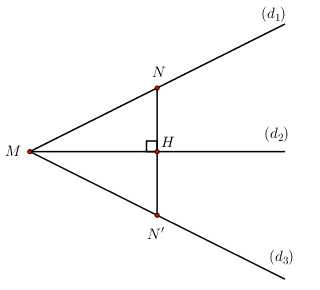
Giải hệ \(\left\{ \begin{array}{l}\left( {{d_1}} \right)\\\left( {{d_2}} \right)\end{array} \right. \Rightarrow M\left( {1;1} \right)\)
Từ phương trình \(\left( {{d_1}} \right)\) cho
\(y = 3 \Rightarrow x = - 2 \Rightarrow N\left( { - 2;3} \right) \in \left( {{d_1}} \right)\)
* Lập phương trình NH đi qua N và vuông góc với \(\left( {{d_2}} \right)\).
\(NH \bot \left( {{d_2}} \right) \Rightarrow \) Phương trình \(\left( {NH} \right):\,\,x - y + c = 0\)
\(N\left( { - 2;3} \right) \in NH \Rightarrow - 2 - 3 + c = 0 \Leftrightarrow c = 5\)
\( \Rightarrow \) Phương trình \(\left( {NH} \right):\,\,x - y + 5 = 0\)
Giải hệ \(\left\{ \begin{array}{l}NH\\\left( {{d_2}} \right)\end{array} \right. \Rightarrow H\left( { - \frac{3}{2};\frac{7}{2}} \right) \Rightarrow N'\left( { - 1;4} \right)\)
* Lập phương trình đường thẳng \(\left( {{d_3}} \right)\)
\(\left( {{d_3}} \right)\) qua M, N’ có phương trình \(\frac{{x - 1}}{{ - 2}} = \frac{{y - 1}}{3} \Leftrightarrow 3x + 2y - 5 = 0\).
