Cho hai dây dẫn thẳng, dài, song song và một khung dây hình chữ nhật c
Câu hỏi
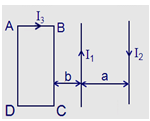
Nhận biếtCho hai dây dẫn thẳng, dài, song song và một khung dây hình chữ nhật cùng nằm trong một mặt phẵng đặt trong không khí và có các dòng điện chạy qua như hình vẽ.

Biết I1 = 15A; I2 = 10A; I3 = 4A; a = 15cm; b = 10 cm; AB = 15 cm; BC = 20cm. Xác định lực từ do từ trường của hai dòng điện chạy trong hai dây dẫn thẳng tác dụng lên cạnh BC của khung dây.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
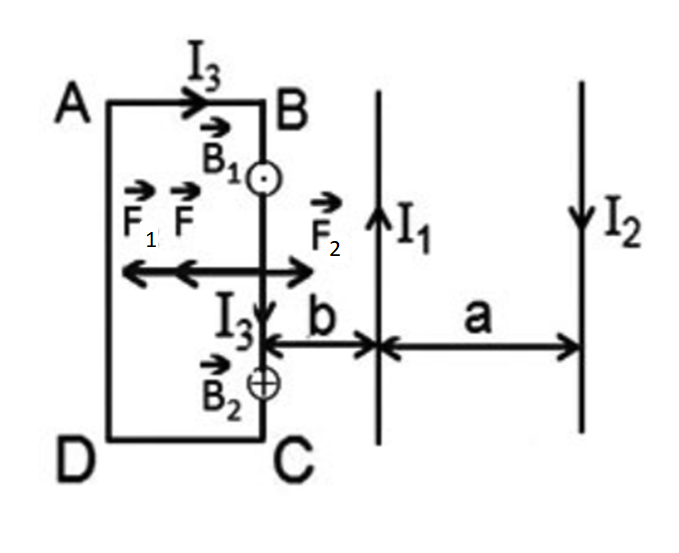
Dòng I1 gây ra tại các điểm trên cạnh BC của khung dây vecto cảm ứng từ có phương vuông góc với mặt phẳng hình vẽ, có chiều hướng từ trong ra và có độ lớn: \({{B}_{1}}={{2.10}^{-7}}\frac{{{I}_{1}}}{b}\)
Từ trường của dòng I1 tác dụng lên cạnh BC lực từ \(\overrightarrow{{{F}_{1}}}\) đặt tại trung điểm của cạnh BC, có phương nằm trong mặt phẳng hình vẽ, vuông góc với BC, hướng từ phải sang trái và có độ lớn:
\({{F}_{1}}={{B}_{1}}{{I}_{3}}BC.\sin {{90}^{0}}={{2.10}^{-7}}.\frac{{{I}_{1}}{{I}_{3}}.BC}{a}=2,{{4.10}^{-5}}\,\,\left( N \right)\)
Lập luận tương tự, ta thấy từ trường của dòng I2 tác dụng lên cạnh BC lực từ \(\overrightarrow{{{F}_{2}}}\) có cùng điểm đặt, cùng phương, ngược chiều với \(\overrightarrow{{{F}_{1}}}\) và có độ lớn:
\({{F}_{2}}={{2.10}^{-7}}.\frac{{{I}_{2}}{{I}_{3}}.BC}{a+b}=6,{{4.10}^{-6}}\,\,\left( N \right)\)
Lực từ tổng hợp do từ trường của hai dòng điện I1 và I2 tác dụng lên cạnh BC của khung dây là:
\(F={{F}_{1}}-{{F}_{2}}=2,{{4.10}^{-5}}-6,{{4.10}^{-6}}=1,{{76.10}^{-5}}\,\,\left( N \right)\)
Luyện tập
Câu hỏi liên quan
-





Đặt một hiệu điện thế U không đổi vào hai cực của bình điện phân. Xét trong cùng một khoảng thời gian, nếu kéo hai cực của bình ra xa sao cho khoảng cách giữa chúng tăng gấp 2 lần thì khối lượng chất được giải phóng ở điện cực so với lúc trước sẽ:

Khi tăng nhiệt độ của một kim loại sẽ làm tăng điện trở của kim loại này, nguyên nhân gây ra hiện hượng này là:

