Cho góc góc xAy = 60^o và ( O ) là đường tròn tiếp xúc với tia Ax tại

Câu hỏi
Nhận biếtCho góc \(\angle xAy = {60^o}\) và \(\left( O \right)\) là đường tròn tiếp xúc với tia Ax tại B và tiếp xúc với tia Ay tại C. Trên cung nhỏ \(BC\) của đường tròn \(\left( O \right)\) lấy điểm M và gọi D, E, F lần lượt là hình chiếu vuông góc của M trên BC, CA, AB.
a) Chứng minh tứ giác CDME là tứ giác nội tiếp.
b) Tính số đo của góc \(\angle EDF\).
c) Chứng minh rằng \(M{D^2} = ME.MF\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
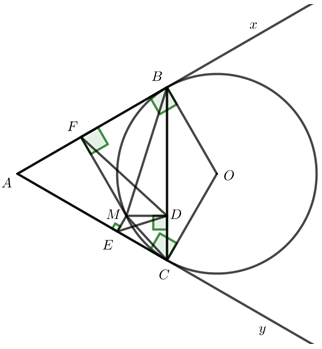
a) Chứng minh tứ giác CDME là tứ giác nội tiếp.
Ta có: \(\angle CDM = {90^o}\,\,\,\left( {MD \bot BC} \right)\) và \(\angle CEM = {90^o}\,\,\left( {ME \bot AC} \right)\)
\( \Rightarrow \angle CDM + \angle CEM = {180^o}\)
\( \Rightarrow \) CDME là tứ giác nội tiếp (dhnb). (đpcm)
b) Tính số đo của góc \(\angle EDF\).
Ta có \(\angle MDE = \angle MCE\) (hai góc nội tiếp cùng chắn cung EC).
Mà \(\angle MCE = \angle MBC\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung MC của \(\left( O \right)\)) \( \Rightarrow \angle MDE = \angle MBC\,\,\,\left( { = \angle MCE} \right)\,\,\,\left( 1 \right)\)
Tương tự câu a) ta cũng có BDMF là tứ giác nội tiếp \( \Rightarrow \angle MDF = \angle MBF\,\,\left( { = \angle MBC} \right)\,\,\,\,\,\,\left( 2 \right)\)
\(\Delta ABC\) có \(AB = AC\) (tính chất hai tiếp tuyến cắt nhau) và \(\angle BAC = {60^o}\,\,\,\left( {gt} \right) \Rightarrow \Delta ABC\) là tam giác đều.
Từ (1) và (2) \( \Rightarrow \angle EDF = \angle MDE + \angle MDF = \angle MBC + \angle MBF = \angle CBA = {60^o}\) (\(\Delta ABC\) đều)
c) Chứng minh rằng \(M{D^2} = ME.MF\).
Ta có \(\angle MED = \angle MCD\) (hai góc nội tiếp cùng chắn cung MD).
Mà \(\angle MCD = \angle MBF\) (góc nội tiếp và góc tạo bởi tia tiếp tuyến và dây cung cùng chắn cung BM)
Kết hợp (2) \( \Rightarrow \angle MED = \angle MDF\,\,\,\left( { = \angle MBF} \right)\)
Ta có \(\angle MBC = \angle MFD\) (BDMF là tứ giác nội tiếp, hai góc nội tiếp cùng chắn cung MD)
Kết hợp (1) \( \Rightarrow \angle MDE = \angle MFD\,\,\,\left( {\angle MBC} \right).\)
Xét \(\Delta MDE\) và \(\Delta MFD\) ta có:
\(\begin{array}{l}\angle MED = \angle MDF\,\,\,\left( {cmt} \right)\\\angle MDE = \angle MFD\,\,\,\,\left( {cmt} \right)\\ \Rightarrow \Delta MDE \sim \Delta MFD\,\,\,\left( {g - g} \right)\\ \Rightarrow \frac{{MD}}{{MF}} = \frac{{ME}}{{MD}} \Rightarrow M{D^2} = ME.MF\,\,\,\,\left( {dpcm} \right)\end{array}\)

