Cho elip (E):13x^2 + 16y^2 = 208. Tìm tọa độ các điểm A B trên (E) và đối xứng nhau qua Ox (điểm A c

Câu hỏi
Nhận biếtCho elip \((E):13{x^2} + 16{y^2} = 208\). Tìm tọa độ các điểm A, B trên (E) và đối xứng nhau qua Ox (điểm A có tung độ dương) sao cho \(AB{F_1}\) là tam giác đều.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
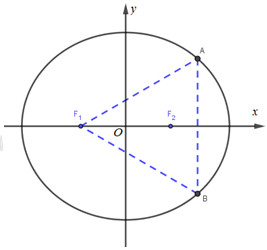
Giả sử \(A({x_0};{y_0}),\,\,{y_0} > 0\). Do A, B đối xứng nhau qua Ox nên \(B({x_0}; - {y_0})\).
\((E):13{x^2} + 16{y^2} = 208 \Leftrightarrow {{{x^2}} \over {16}} + {{{y^2}} \over {13}} = 1 \Rightarrow a = 4,\,\,b = \sqrt {13} \Rightarrow c = \sqrt 3 \)
\( \Rightarrow {F_1}\left( { - \sqrt 3 ;0} \right)\)
Ta có: \(A{B^2} = 4{y_0}^2,\,\,\,A{F_1}^2 = {\left( {{x_0} + \sqrt 3 } \right)^2} + {y_0}^2\)
Vì \(A \in \left( E \right) \Rightarrow 13{x_0}^2 + 16{y_0}^2 = 208 \Rightarrow {y_0}^2 = 13 - {{13} \over {16}}{x_0}^2\,\,(1)\)
Vì tam giác \(AB{F_1}\) là tam giác đều \( \Rightarrow AB = A{F_1} \Rightarrow {\left( {{x_0} + \sqrt 3 } \right)^2} + {y_0}^2 = 4{y_0}^2\,\,\,(2)\)
Thay (1) vào (2) ta được : \({\left( {{x_0} + \sqrt 3 } \right)^2} + 13 - {{13} \over {16}}{x_0}^2 = 4\left( {13 - {{13} \over {16}}{x_0}^2} \right) \Leftrightarrow {{55} \over {16}}{x_0}^2 + 2\sqrt 3 {x_0} - 36 = 0 \Leftrightarrow \left[ \matrix{ {x_0} = {{8\sqrt 3 } \over 5} \hfill \cr {x_0} = {{ - 24\sqrt 3 } \over {11}} \hfill \cr} \right.\)
+) \({x_0} = {{8\sqrt 3 } \over 5} \Rightarrow \left[ \matrix{ {y_0} = {{13} \over 5} \hfill \cr {y_0} = - {{13} \over 5}\,(L) \hfill \cr} \right. \Rightarrow A\left( {{{8\sqrt 3 } \over 5};{{13} \over 5}} \right),\,B\left( {{{8\sqrt 3 } \over 5}; - {{13} \over 5}} \right)\,\)
+) \({x_0} = {{ - 24\sqrt 3 } \over {11}} \Rightarrow \left[ \matrix{ {y_0} = {{13} \over {11}} \hfill \cr {y_0} = - {{13} \over {11}}\,(L) \hfill \cr} \right. \Rightarrow A\left( { - {{24\sqrt 3 } \over {11}};{{13} \over {11}}} \right),\,B\left( { - {{24\sqrt 3 } \over {11}}; - {{13} \over {11}}} \right)\,\)
Vậy, \(A\left( {{{8\sqrt 3 } \over 5};{{13} \over 5}} \right),\,B\left( {{{8\sqrt 3 } \over 5}; - {{13} \over 5}} \right)\,\) hoặc \(A\left( { - {{24\sqrt 3 } \over {11}};{{13} \over {11}}} \right),\,B\left( { - {{24\sqrt 3 } \over {11}}; - {{13} \over {11}}} \right)\,\).
Chọn: B.
