Cho đường tròn tâm ( O;R ) có đường kính AB vuông góc với dây cung MN
Câu hỏi
Nhận biếtCho đường tròn tâm \(\left( O;R \right)\) có đường kính AB vuông góc với dây cung MN tại H (H nằm giữa O và B). Trên tia MN lấy điểm C nằm ngoài đường tròn \(\left( O;R \right)\) sao cho đoạn thẳng AC cắt đường tròn \(\left( O;R \right)\) tại điểm K (K khác A), hai dây MN và BK cắt nhau ở E.
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
b) Chứng minh CA.CK = CE.CH
c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.
d) Khi KE = KC. Chứng minh OK // MN.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
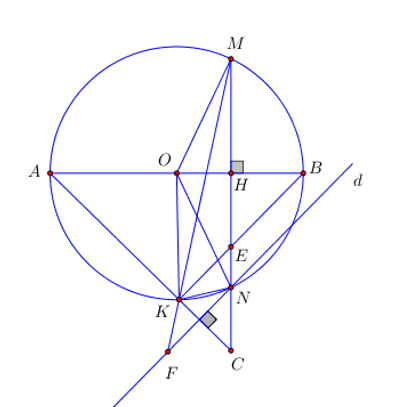
a) Chứng minh rằng tứ giác AHEK là tứ giác nội tiếp.
Ta có \(\widehat{AKB}={{90}^{0}}\) (góc nội tiếp chắn nửa đường tròn) \(\Rightarrow \widehat{AKE}={{90}^{0}}\)
Xét tứ giác AHEK có \(\widehat{AKE}+\widehat{AHE}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\Rightarrow \) tứ giác AHEK là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
b) Chứng minh CA.CK = CE.CH
Xét tam giác CKE và tam giác CHA có:
\(\widehat{CKE}=\widehat{CHA}={{90}^{0}};\)
\(\widehat{ACH}\) chung;
\(\Rightarrow \Delta CKE\backsim \Delta CHA\,\,\left( g.g \right)\Rightarrow \frac{CK}{CH}=\frac{CE}{CA}\Rightarrow CA.CK=CE.CH\)(đpcm).
c) Qua điểm N kẻ đường thẳng (d) vuông góc với AC, (d) cắt MK tại F. Chứng minh tam giác NFK cân.
Ta có \(d\bot AC;\,\,\widehat{AKB}={{90}^{0}}\Rightarrow BK\bot AK\Rightarrow BK\bot AC\Rightarrow d//BK\). (từ vuông góc đến song song).
Xét tam giác OMN có \(OM=ON\left( =R \right)\Rightarrow \Delta OMN\) cân tại O.
\(\Rightarrow \) Đường cao OH đồng thời là đường phân giác \(\Rightarrow \widehat{MOB}=\widehat{NOB}\Rightarrow \) sđ cung MB = sđ cung NB.
\(\Rightarrow \widehat{MKB}=\widehat{NKB}\) (hai góc nội tiếp chắn hai cung bằng nhau).
Ta có \(\widehat{KFN}=\widehat{MKB}\) (đồng vị);
\(\widehat{KNF}=\widehat{NKB}\) (so le trong);
Mà \(\widehat{MKB}=\widehat{NKB}\,\,\left( cmt \right)\Rightarrow \widehat{KFN}=\widehat{KNF}\Rightarrow \Delta NEK\) cân tại K.
d) Khi KE = KC. Chứng minh OK // MN.
Ta có \(\widehat{AKB}={{90}^{0}}\Rightarrow BK\bot AK\Rightarrow BK\bot AC\Rightarrow \Delta KEC\) vuông tại K.
Lại có KE = KC (gt) \(\Rightarrow \Delta KEC\) vuông cân tại K \(\Rightarrow \widehat{KEC}={{45}^{0}}\) ;
\(\Rightarrow \widehat{HEB}=\widehat{KEC}={{45}^{0}}\) (đối đỉnh) \(\Rightarrow \Delta HEB\) vuông cân tại H \(\Rightarrow \widehat{HBE}={{45}^{0}}\Rightarrow \widehat{OBK}={{45}^{0}}\)
Tam giác OBK có \(OB=OK\ \left( =R \right)\Rightarrow \Delta OBK\) cân tại O \(\Rightarrow \widehat{OBK}=\widehat{OKB}={{45}^{0}}\)
\(\Rightarrow \widehat{BOK}={{180}^{0}}-{{45}^{0}}-{{45}^{0}}={{90}^{0}}\Rightarrow \Delta BOK\) vuông cân tại \(O\Rightarrow OK\bot OB\) ;
Lại có \(MN\bot AB\,\,\left( gt \right)\Rightarrow MN\bot OB\).
Vậy MN // OK.
