Cho đường tròn tâm O, đường kính AB và điểm C nằm trên đường tròn (C k

Câu hỏi
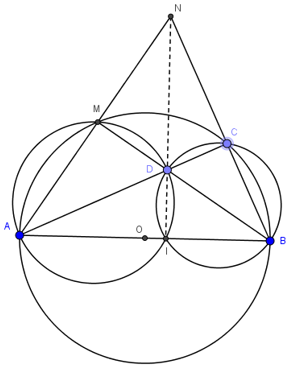
Nhận biếtCho đường tròn tâm O, đường kính AB và điểm C nằm trên đường tròn (C không trùng với A và B). Lấy điểm D thuộc đoạn AC (D không trùng với A và C). Tia BD cắt cung nhỏ AC tại điểm M, tia BC cắt tia AM tại điểm N.
1. Chứng minh MNCD là tứ giác nội tiếp.
2. Chứng minh AM.BD = AD.BC
3. Gọi I là giao điểm thứ hai của đường tròn ngoại tiếp tam giác ADM và tam giác BDC. Chứng minh ba điểm N, D, I thẳng hàng.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
1. \(\widehat{AMB}=\widehat{ACB}={{90}^{0}}\) (Góc nội tiếp chắn nửa đường tròn) \(\Rightarrow \widehat{NMD}=\widehat{NCD}={{90}^{0}}\)
Do đó tứ giác MNCD là tứ giác nội tiếp (Tứ giác có tổng 2 góc đối bằng \({{180}^{0}}\) )
2. Xét hai tam giác AMD và BCD có \(\widehat{AMD}=\widehat{BCD}={{90}^{0}}\) ,\(\widehat{ADM}=\widehat{BDC}\) (đối đỉnh) Nên \(\Delta AMD\sim \Delta BCD\left( g.g \right)\Rightarrow \frac{AM}{BC}=\frac{AD}{BD}\Rightarrow AM.BD=AD.BC\)
3.
+) Xét tam giác NAC và NBM có: \(\widehat{CNA}\) chung \(\widehat{NAC}=\widehat{NBM}\) (2 góc nội tiếp cùng chắn cung NC)
Suy ra \(\Delta NAC\sim \Delta NBM\left( g.g \right)\Rightarrow \frac{NA}{NB}=\frac{NC}{NM}\)(2 cặp cạnh tương ứng tỉ lệ)
+) Xét tam giác NAB và NCM có: \(\widehat{ANB}\) chung \(\frac{NA}{NB}=\frac{NC}{NM}\)(cmt)
Suy ra \(\Delta NAB\sim \Delta NCM\left( c.g.c \right)\) \(\Rightarrow \widehat{NAB}=\widehat{NCM}\) (2 góc tương ứng)
Mà \(\widehat{NCM}=\widehat{NDM}\)(2 góc nội tiếp cùng chắn cung NM) suy ra\(\widehat{NAB}=\widehat{NDM}\)
Vì tứ giác AMDI nội tiếp nên \(\widehat{NAB}+\widehat{MDI}={{180}^{0}}\Rightarrow \widehat{NDM}+\widehat{MDI}={{180}^{0}}\Rightarrow \widehat{NDI}={{180}^{0}}\)
Vậy N, D, I thẳng hàng.

