Cho đường tròn tâm ( O ), đường kính AB = 2R. Gọi d1;d2 lần lượt là cá

Lời giải của Tự Học 365

Giải chi tiết:

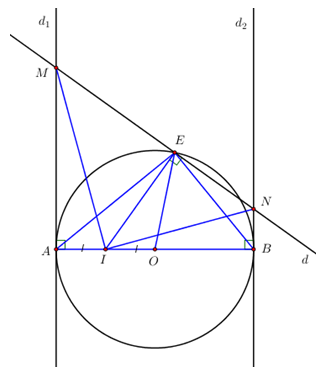
Cho đường tròn tâm \(\left( O \right)\), đường kính \(AB = 2R\). Gọi \({d_1};{d_2}\) lần lượt là các tiếp tuyến của đường tròn \(\left( O \right)\) tại A và B, I là trung điểm của đoạn thẳng OA, E là điểm thay đổi trên đường tròn \(\left( O \right)\) sao cho E không trùng với A và B. Đường thẳng d đi qua E và vuông góc với đường thẳng EI cắt \({d_1};{d_2}\) lần lượt tại M, N.

1. Chứng minh AMEI là tứ giác nội tiếp.

Ta có: MA là tiếp tuyến của (O) tại A nên \(\angle IAM = {90^0}\)

Xét tứ giác \(AMEI\) có \(\angle IAM + \angle IEM = {90^0} + {90^0} = {180^0}\)

\( \Rightarrow \)  Tứ giác \(AMEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰)

2. Chứng minh \(IB.NE = 3IE.NB\)

Ta có \(\angle IEA + \angle IEB = \angle AEB = {90^0}\) (góc nội tiếp chắn nửa đường tròn);

\(\angle NEB + \angle IEB = \angle NEI = {90^0}\,\,\left( {gt} \right)\);

\( \Rightarrow \angle IEA = \angle NEB\)

Xét \(\Delta IEA\) và \(\Delta NEB\) có:

\(\angle IEA = \angle NEB\,\,\left( {cmt} \right)\);

\(\angle IAE = \angle BAE = \angle NBE\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung BE);

\( \Rightarrow \Delta IEA \sim \Delta NEB\,\,\left( {g.g} \right) \Rightarrow \frac{{IE}}{{IA}} = \frac{{NE}}{{NB}} \Rightarrow IA.NE = IE.NB \Rightarrow 3IA.NE = 3IE.NB\)

Do I là trung điểm của OA \( \Rightarrow IA = \frac{1}{2}OA = \frac{1}{2}.\frac{1}{2}AB = \frac{1}{4}AB \Rightarrow IA = \frac{1}{3}IB\) hay \(IB = 3IA\).

\( \Rightarrow IB.NE = 3IE.NB\,\,\left( {dpcm} \right)\).

3. Khi điểm E thay đổi chứng minh tích \(AM.BN\) có giá trị không đổi và tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R.

+) Chứng minh tích \(AM.BN\) có giá trị không đổi

Xét tứ giác \(BNEI\) có \(\angle IBN + \angle IEN = {90^0} + {90^0} = {180^0} \Rightarrow \) Tứ giác \(BNEI\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 180⁰)

\( \Rightarrow \angle NEB = \angle NIB\) (hai góc nội tiếp cùng chắn cung NB)

Ta có \(\angle AMI = \angle AEI\) (hai góc nội tiếp cùng chắn cung AI) ;

Mà \(\angle AEI = \angle NEB\,\,\left( {cmt} \right)\)

\( \Rightarrow \angle AMI = \angle NIB\).

Xét \(\Delta AMI\) và \(\Delta BIN\) có:

\(\begin{array}{l}\angle AMI = \angle NIB\,\,\left( {cmt} \right);\\\angle MAI = \angle IBN = {90^0}\,\,\left( {gt} \right);\\ \Rightarrow \Delta AMI \sim \Delta BIN\,\,\left( {g.g} \right) \Rightarrow \frac{{AM}}{{BI}} = \frac{{AI}}{{BN}} \Rightarrow AM.BN = AI.BI\end{array}\)

Ta có \(AI = \frac{1}{4}AB = \frac{1}{4}.2R = \frac{R}{2};\,\,BI = \frac{3}{4}AB = \frac{3}{4}.2R = \frac{{3R}}{2}\) 

\( \Rightarrow AM.BN = \frac{R}{2}.\frac{{3R}}{2} = \frac{{3{R^2}}}{4} = const\).

+) Tìm giá trị nhỏ nhất của diện tích tam giác MNI theo R.

Tứ giác BNEI là tứ giác nội tiếp (cmt) \( \Rightarrow \angle ENI = \angle EBI\) (hai góc nội tiếp cùng chắn cung EI)

Do tứ giác \(AMEI\) nội tiếp (cmt) \( \Rightarrow \angle IME = \angle IAE\) (hai góc nội tiếp cùng chắn cung IE)

\( \Rightarrow \angle ENI = \angle IME = \angle EBI + \angle IAE = {90^0}\) (\(\Delta ABE\) vuông tại E)

\( \Rightarrow \angle MIN = {90^0} \Rightarrow \Delta IMN\) vuông tại I \( \Rightarrow {S_{IMN}} = \frac{1}{2}IM.IN\)

Đặt \(\angle AIM = \alpha  \Rightarrow \angle BNI = \alpha \,\,\left( {{0^0} < \alpha  < {{90}^0}} \right)\left( {Do\,\,\Delta AMI \sim \Delta BIN} \right)\).

Xét tam giác vuông AIM có \(\cos \angle AIM = \cos \alpha  = \frac{{AI}}{{MI}} \Rightarrow MI = \frac{{AI}}{{\cos \alpha }} = \frac{{\frac{R}{2}}}{{\cos \alpha }} = \frac{R}{{2\cos \alpha }}\)

Xét tam giác vuông BIN có : \(\sin \angle BNI = \sin \alpha  = \frac{{BI}}{{IN}} \Rightarrow IN = \frac{{BI}}{{\sin \alpha }} = \frac{{\frac{{3R}}{2}}}{{\sin \alpha }} = \frac{{3R}}{{2\sin \alpha }}\)

\( \Rightarrow {S_{IMN}} = \frac{1}{2}IM.IN = \frac{1}{2}.\frac{R}{{2\cos \alpha }}.\frac{{3R}}{{2\sin \alpha }} = \frac{{3{R^2}}}{{8\sin \alpha \cos \alpha }}\)

Do \({0^0} < \alpha  < {90^0} \Rightarrow \sin \alpha  > 0,\,\,\cos \alpha  > 0\) và \(\cos \alpha  = \sqrt {1 - {{\sin }^2}\alpha } \).

\(\begin{array}{l} \Rightarrow \sin \alpha .\cos \alpha  = \sin \alpha .\sqrt {1 - {{\sin }^2}\alpha } \mathop  \le \limits^{Cauchy} \frac{{{{\sin }^2}\alpha  + 1 - {{\sin }^2}\alpha }}{2} = \frac{1}{2}\\ \Rightarrow {S_{IMN}} \ge \frac{{3{R^2}}}{{8.\frac{1}{2}}} = \frac{{3{R^2}}}{4}\end{array}\)

Dấu bằng xảy ra \( \Leftrightarrow \sin \alpha  = \sqrt {1 - {{\sin }^2}\alpha }  \Leftrightarrow 2{\sin ^2}\alpha  = 1 \Leftrightarrow \sin \alpha  = \frac{1}{{\sqrt 2 }} \Leftrightarrow \alpha  = {45^0}\)

Vậy \({S_{IMN\,\,\min }} = \frac{{3{R^2}}}{4} \Leftrightarrow \angle AIM = {45^0}\).