Cho đường tròn tâm O dây AB = 24cm dây AC = 20cm (góc BAC < 90^0 và điểm O nằm trong góc BAC). Gọi

Câu hỏi
Nhận biếtCho đường tròn tâm \(O,\) dây \(AB = 24cm,\) dây \(AC = 20cm\) (\(\widehat {BAC} < {90^0}\) và điểm \(O\) nằm trong góc \(BAC\)). Gọi \(M\) là trung điểm \(AC.\) Khoảng cách từ \(M\) đến \(AB\) bằng \(8cm.\) Tính bán kính của đường tròn.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
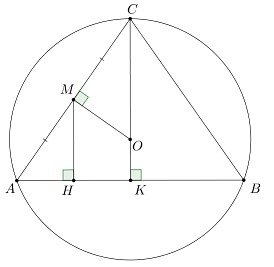
Kẻ \(MH \bot AB\) tại \(H.\) Khi đó \(AM = 10cm,\,\,MH = 8cm.\)
Áp dụng định lý Pytago cho tam giác \(AMH\) vuông tại \(H:\)
\(\begin{array}{l}A{M^2} = M{H^2} + A{H^2} \Rightarrow {10^2} = {8^2} + A{H^2}\\ \Rightarrow A{H^2} = 36 \Rightarrow AH = 6\,\,\,\,\left( {cm} \right).\end{array}\)
Kẻ \(CK \bot AB\) tại \(K.\)
Ta có: \(MH\) // \(CK\) (cùng vuông góc với \(AB\)), \(M\) là trung điểm \(AC\), suy ra \(H\) là trung điểm \(AK\).
Do đó \(AK = 2AH = 12cm = \dfrac{1}{2}AB.\)
Như vậy, \(CK\) vừa là đường cao, vừa là trung tuyến của tam giác \(ABC,\) cho nên \(\Delta ABC\) cân tại \(C.\)
Do đó, \(O\) nằm trên \(CK.\)
Lại có \(MH\) là đường trung bình của tam giác \(ACK,\) suy ra \(CK = 2MH = 16cm.\)
Xét tam giác \(CMO\) và tam giác \(CKA.\) Ta có: \(\widehat C\) chung và \(\widehat {CMO} = \widehat {CKA} = {90^0}.\)
Suy ra \( \Rightarrow \Delta CMO \sim \Delta CKA\,\,\left( {g - g} \right)\)\( \Rightarrow \dfrac{{CM}}{{CK}} = \dfrac{{CO}}{{CA}} \Rightarrow \dfrac{{10}}{{16}} = \dfrac{R}{{20}} \Rightarrow R = 12,5\,\,\,\left( {cm} \right).\)
Vậy \(R = 12,5\,\,cm\).
Chọn B.

