Cho đường tròn tâm O bán kính R. Từ điểm C nằm ngoài đường tròn kẻ hai

Câu hỏi
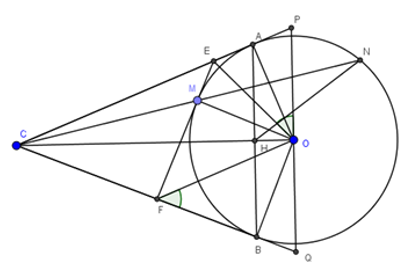
Nhận biếtCho đường tròn tâm O bán kính R. Từ điểm C nằm ngoài đường tròn kẻ hai tiếp tuyến CA, CB và cát tuyến CMN với đường tròn (O) (A, B là hai tiếp điểm, M là điểm nằm giữa C và N). Gọi H là giao điểm của CO và AB
a) Chứng minh tứ giác AOBC nội tiếp
b) Chứng minh rằng \(CH.CO=CM.CN\)
c) Tiếp tuyến tại M của đường tròn (O) cắt CA, CB theo thứ tự E, F. Đường thẳng vuông góc với CO tại O cắt CA, CB theo thứ tự tại P và Q. Chứng minh \(\widehat{POE}=\widehat{OFQ}\)
d) Chứng minh rằng \(PE+QF\ge PQ\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Vì CA và CB là các tiếp tuyến của đường tròn (O) nên \(\widehat{CAO}=\widehat{CBO}={{90}^{0}}\Rightarrow \widehat{CAO}+\widehat{CBO}={{180}^{0}}\)
b) Xét tam giác ACM và NCA có \(\widehat{ACN}\) chungVậy tứ giác AOBC là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
\(\widehat{CAM}=\widehat{ANM}\) (cùng chắn cung AM)
\(\Rightarrow \Delta ACM\sim \Delta NCA\left( g.g \right)\Rightarrow \frac{AC}{NC}=\frac{CM}{AC}\Rightarrow A{{C}^{2}}=CM.CN\)
Xét tam giác vuông OAC có\(A{{C}^{2}}=CH.CO\)
Từ đó suy ra \(CH.CO=CM.CN\)
\(\begin{align} & c)\ \ \,\widehat{OFQ}=\widehat{OCF}+\widehat{COF}=\widehat{OCP}+\widehat{COF}=\widehat{AOP}+\widehat{COF} \\ & +)\,\widehat{POE}=\widehat{POA}+\widehat{AOE}=\widehat{AOP}+\frac{1}{2}\widehat{AOM}=\widehat{AOP}+\frac{1}{2}\left( {{180}^{0}}-\widehat{AEM} \right) \\ & \,\,\,\,\,\,\,\,\,\,\,=\widehat{AOP}+{{90}^{o}}-\frac{1}{2}\left( \widehat{ECF}+\widehat{CFE} \right)=\widehat{AOP}+{{90}^{o}}-\frac{1}{2}\left( {{180}^{0}}-\widehat{AOB} \right)-\frac{1}{2}\left( {{180}^{o}}-\widehat{MFB} \right) \\ & \,\,\,\,\,\,\,\,\,\,\,\,=\widehat{AOP}+\frac{1}{2}\widehat{AOB}-\frac{1}{2}\left( {{180}^{0}}-{{180}^{0}}+\widehat{\mathbf{M}OB} \right)=\widehat{AOP}+\widehat{COB}-\widehat{BOF}=\widehat{AOP}+\widehat{COF} \\ \end{align}\)
Vậy \(\widehat{POE}=\widehat{OFQ}\)
d) Tam giác CPQ cân tại C\(\Rightarrow \widehat{OPE}=\widehat{FQO}\) , và \(\widehat{POE}=\widehat{OFQ}\)(cmt) nên \(\Delta PEO\sim \Delta QOF\left( g.g \right)\)
\(\Rightarrow \frac{PE}{QO}=\frac{PO}{QF}\Rightarrow PE.QF=PO.QO={{\left( \frac{PQ}{2} \right)}^{2}}\)
Áp dụng bất đẳng thức Cô si có: \(PE+QF\ge 2\sqrt{PE.QF}=2\sqrt{{{\left( \frac{PQ}{2} \right)}^{2}}}=PQ\)

