Cho đường tròn tâm O bán kính R đường kính BC. Gọi A là một điểm thuộc đường tròn (A khác B và C). Đ

Câu hỏi
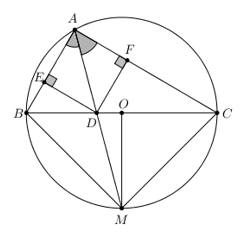
Nhận biếtCho đường tròn tâm O bán kính R, đường kính BC. Gọi A là một điểm thuộc đường tròn (A khác B và C). Đường phân giác của góc BAC cắt BC tại D và cắt đường tròn tại M.
1. Chứng minh MB = MC và OM vuông góc với BC.
2. Gọi E, F lần lượt là hình chiếu của D lên AB, AC. Tứ giác AEDF là hình gì ?
3. Cho góc \(ABC = 60^0\). Tính diện tích tam giác MDC theo R.
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
1. Do AM là phân giác của góc BAC \(\Rightarrow \widehat{MAB}=\widehat{MAC}\Rightarrow \) sđ cung MB = sđ cung MC.
\(\Rightarrow MB=MC\) (hai dây cung chắn hai góc bằng nhau thì bằng nhau).
\(\Rightarrow \Delta MBC\) cân tại M \(\Rightarrow \) Trung tuyến MO đồng thời là đường cao \(\Rightarrow MO\bot BC\).
2. Ta có \(\widehat{BAC}={{90}^{0}}\Rightarrow \widehat{EAF}={{90}^{0}}\) (góc nội tiếp chắn nửa đường tròn)
\(DE\bot AB\Rightarrow \widehat{DEA}={{90}^{0}};\,\,DF\bot AC\Rightarrow \widehat{DFA}={{90}^{0}}\Rightarrow \) Tứ giác AEDF là hình chữ nhật (Tứ giác có ba góc vuông).
Lại có \(AD\) là phân giác của góc EAF \(\Rightarrow \) AEDF là hình vuông (Hình chữ nhật có 1 đường chéo đồng thời là phân giác của 1 góc).
3. Ta có: \(\widehat{ABC}={{60}^{0}}\Rightarrow AB=R,\ \ AC=R\sqrt{3}.\ \ \)
Vì AD là phân giác của góc BAC
\(\Rightarrow \frac{DB}{DC}=\frac{AB}{AC}=\frac{R}{R\sqrt{3}}=\frac{1}{\sqrt{3}}\Rightarrow \frac{DB+DC}{DC}=\frac{1+\sqrt{3}}{\sqrt{3}}\Rightarrow \frac{BC}{DC}=\frac{1+\sqrt{3}}{\sqrt{3}}\)
\(\Rightarrow DC=\frac{BC\sqrt{3}}{1+\sqrt{3}}=\frac{2R\sqrt{3}}{1+\sqrt{3}}=\left( 3-\sqrt{3} \right)R\)
\(\Rightarrow {{S}_{MDC}}=\frac{1}{2}OM.DC=\frac{1}{2}R.\left( 3-\sqrt{3} \right)R=\frac{\sqrt{3}\left( \sqrt{3}-1 \right)}{2}{{R}^{2}}\)
Chọn C

