Cho đường tròn tâm O bán kính 2R (kí hiệu (O; 2R)) và đường tròn tâm O’ bán kính R (kí hiệu (O’; R))

Câu hỏi
Nhận biếtCho đường tròn tâm O bán kính 2R (kí hiệu (O; 2R)) và đường tròn tâm O’ bán kính R (kí hiệu (O’; R)) tiếp xúc ngoài nhau tại A. Lấy điểm B trên đường tròn (O; 2R) sao cho \(\widehat{BAO}={{30}^{0}}\), tia BA cắt đường tròn (O’; R) tại điểm C (C khác điểm A). Tiếp tuyến của đường tròn (O’; R) tại điểm C cắt đường thẳng BO tại điểm E. Tính theo R diện tích tam giác ABE.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
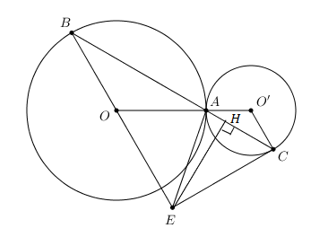
Tam giác OAB có \(OA=OB\Rightarrow \Delta OAB\) cân tại \(O\Rightarrow \widehat{OAB}=\widehat{OBA}={{30}^{0}}\)
Xét tam giác OAB có \(\widehat{AOB}={{180}^{0}}-{{30}^{0}}-{{30}^{0}}={{120}^{0}}\).
Tam giác O’AC có O’A = O’C \(\Rightarrow \Delta O'AC\) cân tại O’ \(\Rightarrow \widehat{O'CA}=\widehat{O'AC}=\widehat{OAB}={{30}^{0}}\)
\(\Rightarrow \widehat{OBA}=\widehat{O'CA}={{30}^{0}}\), mà hai góc này ở vị trí so le trong \(\Rightarrow OB//O'C\)
\(\Rightarrow \widehat{AO'C}=\widehat{AOB}={{120}^{0}}\)
Ta có \(\widehat{ACE}=\frac{1}{2}\widehat{AO'C}={{60}^{0}}\)(góc nội tiếp và góc ở tâm cùng chắn cung AC).
Xét tam giác EBC có \(\widehat{OBA}+\widehat{ACE}={{30}^{0}}+{{60}^{0}}={{90}^{0}}\Rightarrow \Delta BCE\) vuông tại E. Ta có \(AC=R\sqrt{3} ;\ AB=2R\sqrt{3}\Rightarrow BC=AB+AC=R\sqrt{3}+2R\sqrt{3}=3R\sqrt{3}.\)
\(\begin{align} & \Rightarrow EC=BC.\cos 60=3R\sqrt{3}.\frac{1}{2}=\frac{3R\sqrt{3}}{2} \\ & \,\,\,\,\,\,BE=BC.\sin {{60}^{0}}=3R\sqrt{3}.\frac{\sqrt{3}}{2}=\frac{9R}{2} \\ \end{align}\)
Kẻ \(EH\bot BC\,\,\left( H\in BC \right)\) ta có \(EH=\frac{EB.EC}{BC}=\frac{\frac{9E}{2}.\frac{3R\sqrt{3}}{2}}{3R\sqrt{3}}=\frac{9R}{4}\)
\(\Rightarrow {{S}_{ABE}}=\frac{1}{2}EH.AB=\frac{1}{2}.\frac{9R}{4}.2R\sqrt{3}=\frac{9\sqrt{3}{{R}^{2}}}{8}\)
Chọn A

