Cho đường tròn ( O;R ) và một đường thẳng d không có điểm chung với đường tròn. Trên d lấy một điểm

Câu hỏi
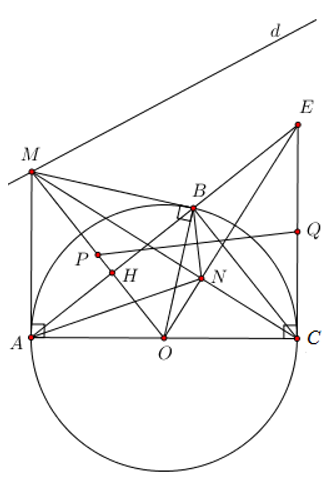
Nhận biếtCho đường tròn \(\left( O;R \right)\) và một đường thẳng d không có điểm chung với đường tròn. Trên d lấy một điểm M bất kì, qua M kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm). Kẻ đường kính AC của đường tròn (O). Tiếp tuyến của đường tròn (O) tại C cắt đường thẳng AB tại E.
a) Chứng minh rằng \(BE.MB=BC.OB\).
b) Gọi N là giao điểm của CM với OE. Chứng minh rằng đường thẳng đi qua trung điểm của đoạn thẳng OM và CE vuông góc với đường thẳng BN.
c) Tìm giá trị nhỏ nhất của dây AB khi điểm M di chuyển trên đường thẳng d, biết R = 8cm và khoảng cách từ O đến đường thẳng d bằng 10cm.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a) Xét tứ giác OAMB có \(\widehat{OAM}+\widehat{OBM}={{90}^{0}}+{{90}^{0}}={{180}^{0}}\Rightarrow \) Tứ giác OAMB là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).
\(\Rightarrow \widehat{OAB}=\widehat{OMB}\) (hai góc nội tiếp cùng chắn cung OB).
Mà \(\widehat{OAB}=\widehat{BCE}\) (cùng phụ với \(\widehat{ACB}\) ) \(\Rightarrow \widehat{OMB}=\widehat{BCE}\) .
Xét tam giác \(OMB\) và tam giác \(ECB\) có:
\(\widehat{OBM}=\widehat{EBC}={{90}^{0}};\,\,\widehat{OMB}=\widehat{BCE}\,\,\left( cmt \right)\Rightarrow \Delta OMB\backsim \Delta ECB\,\,\left( g.g \right)\)
\(\Rightarrow \frac{BE}{OB}=\frac{BC}{MB}\Leftrightarrow BE.MB=BC.OB\) (đpcm).
b) Gọi P và Q lần lượt là trung điểm của OM và CE.
\(\Delta OMB\backsim \Delta ECB\,\,\left( cmt \right)\Rightarrow \widehat{CEB}=\widehat{MOB}\)
Xét tam giác EAC và tam giác OMA có:
\(\begin{align} & \widehat{ECA}=\widehat{OMA}={{90}^{0}};\,\,\widehat{CEA}=\widehat{CEB}=\widehat{MOB}=\widehat{MOA} \ & \Rightarrow \Delta EAC\backsim \Delta OMA\,\,\left( g.g \right)\Rightarrow \frac{EC}{OA}=\frac{AC}{AM}\Rightarrow \frac{EC}{OC}=\frac{AC}{AM}. \ \end{align}\)
Xét tam giác COE và tam giác AMC có \(\widehat{OCE}=\widehat{CAM}={{90}^{0}};\,\,\frac{CE}{CO}=\frac{AC}{AM}\,\,\left( cmt \right)\Rightarrow \Delta COE\backsim \Delta ACM\,\,\left( c.g.c \right)\)
\(\Rightarrow \widehat{AMC}=\widehat{COE}\) . (hai góc tương ứng).
Mà \(\widehat{COE}+\widehat{NOA}={{180}^{0}}\Rightarrow \widehat{AMC}+\widehat{NOA}={{180}^{0}}\Rightarrow \) Tứ giác OAMN là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800). \(\Rightarrow \widehat{ONM}={{180}^{0}}-\widehat{OAM}={{90}^{0}}\Rightarrow \Delta OMN\) vuông tại N.
\(\Rightarrow NP=\frac{1}{2}OM\) (trung tuyến ứng với cạnh huyền trong tam giác vuông).
Ta có \(\Delta OBM\) vuông tại B \(\Rightarrow BP=\frac{1}{2}OM\) (trung tuyến ứng với cạnh huyền trong tam giác vuông).
\(\Rightarrow NP=BP=\frac{1}{2}OM\Rightarrow P\) thuộc trung trực của đoạn thẳng BN.
Chứng minh tương tự ta có \(NQ=BQ=\frac{1}{2}EC\Rightarrow Q\) thuộc trung trực của đoạn thẳng BN.
Vậy PQ là trung trực của đoạn thẳng BN \(\Rightarrow PQ\bot BN\)
c) Gọi \(H=AB\cap OM\) ta có \(OH\bot AB\Rightarrow A{{B}_{\min }}\Leftrightarrow O{{H}_{\max }}\) .
Áp dụng hệ thức lượng trong tam giác vuông OAM có
\(OH.OM=O{{A}^{2}}={{R}^{2}}\Rightarrow OH=\frac{{{R}^{2}}}{OM}\Rightarrow O{{H}_{\max }}\Leftrightarrow O{{M}_{\min }}\Leftrightarrow M\) là hình chiếu vuông góc vủa O trên đường thẳng \(d\Rightarrow OM=d\left( O;d \right)=10\Rightarrow OH=\frac{{{8}^{2}}}{10}=6,4\,\,\left( cm \right)\) .
Xét tam giác vuông OAH có \(AH=\sqrt{{{8}^{2}}-{{6,4}^{2}}}=4,8\,\,\left( cm \right)\Rightarrow AB=2AH=9,6\,\,\left( cm \right)\) .
Vậy dây AM nhỏ nhất là 9,6 cm.
Chọn D

