Cho đường tròn ( O;;R ) và điểm A cố định ở ngoài đường tròn. Vẽ đường
Câu hỏi
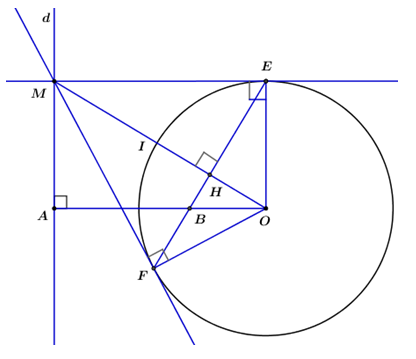
Nhận biếtCho đường tròn \(\left( {O;\;R} \right)\) và điểm \(A\) cố định ở ngoài đường tròn. Vẽ đường tròn đường thẳng \(d\) vuông góc với \(OA\) tại \(A.\) Trên \(d\) lấy điểm \(M.\) Qua \(M\) kẻ hai tiếp tuyến \(ME,\;\;MF\) tới đường tròn \(\left( {O;\;R} \right)\) tiếp điểm lần lượt là \(E\) và \(F.\) Nối \(EF\) cắt \(OM\) tại \(H,\) cắt \(OA\) tại \(B.\)
a) Chứng minh\(OM \bot EF.\)
b) Cho biết \(R = 6cm,\;\;OM = 10cm.\) Tính \(OH.\)
c) Chứng minh bốn điểm \(A,\;\;B,\;\;H,\;\;M\) cùng thuộc một đường tròn.
d) Chứng minh tâm I của đường tròn nội tiếp tam giác \(MEF\) thuộc một đường tròn cố định khi \(M\) chuyển động trên \(d.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Chứng minh\(OM \bot EF.\)
Theo đề bài ta có \(ME,\;\;MF\) là hai tiếp tuyến cắt nhau tại \(M \Rightarrow ME = MF.\) (tính chất)
Xét \(\Delta MFH\) và \(\Delta MEH\) ta có:
\(\begin{array}{l}\angle MFH = \angle MEH = {90^0}\\ME = MF\;\;\left( {cmt} \right)\\MH\;\;chung\\ \Rightarrow \Delta MFH = \Delta MEH\;\;\left( {ch - cgv} \right)\\ \Rightarrow HF = HE\end{array}\)
Xét \(\Delta MEF\) có \(ME = MF \Rightarrow \Delta MEF\) là tam giác cân tại \(M\) có đường trung tuyến \(MH\;\;\left( {do\;\;HE = HF\;\;\left( {cmt} \right)} \right)\)
\( \Rightarrow MH\) cũng là đường cao của \(\Delta MEF\)
\( \Rightarrow MH \bot EF\;\;hay\;\;MO \bot EF.\) (đpcm)
b) Cho biết \(R = 6cm,\;\;OM = 10cm.\) Tính \(OH.\)
Áp dụng hệ thức lượng trong tam giác \(MOE\) vuông tại \(E\) có đường cao \(EH\) ta có:
\(E{O^2} = OH.OM \Leftrightarrow OH = \frac{{E{O^2}}}{{OM}} = \frac{{{6^2}}}{{10}} = 3,6\;cm.\)
c) Chứng minh bốn điểm \(A,\;\;B,\;\;H,\;\;M\) cùng thuộc một đường tròn.
Xét tứ giác \(ABHM\) ta có: \(\angle MAB + \angle BHM = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow ABHM\) là tứ giác nội tiếp (dhnb).
d) Chứng minh tâm I của đường tròn nội tiếp tam giác \(MEF\) thuộc một đường tròn cố định khi \(M\) chuyển động trên \(d.\)
Gọi I là giao điểm của OM và đường tròn \(\left( O \right)\).
Do \(I \in OM \Rightarrow IE = IF \Rightarrow \) sđ cung IE = sđ cung IF.
\( \Rightarrow \angle MFI = \angle IFE\) (góc tạo bởi tiếp tuyến và dây cung và góc nội tiếp chắn các cung bằng nhau).
\( \Rightarrow IF\) là phân giác của góc \(\angle MFE\) (1)
Tam giác MEF cân tại M \(\left( {ME = MF} \right)\), do đó IM là trung trực đồng thời là phân giác của \(\angle EMF\) (2).
Từ (1) và (2) \( \Rightarrow I\) là tâm đường tròn nội tiếp tam giác MEF.
Vậy khi M di chuyển trên đường thẳng d thì I luôn di chuyển trên đường tròn \(\left( O \right)\) cố định (đpcm).
