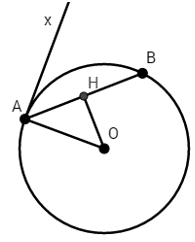
Cho đường tròn ( O;R ) và dây AB=Rcăn 3,Ax là tia tiếp tuyến tại A của

Câu hỏi
Nhận biếtCho đường tròn \( \left( O;R \right) \) và dây \(AB=R \sqrt{3},Ax \) là tia tiếp tuyến tại \(A \) của đường tròn \( \left( O \right) \). Số đo của \( \widehat{xAB} \) (góc chắn cung nhỏ \(AB \)) là
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Lời giải chi tiết.
Kẻ \(OH\) vuông góc với \(AB\) tại \(H\)
Mà \(\Delta AOB\) cân tại \(O\) nên \(H\) là trung điểm của \(AB\)
\(\Rightarrow AH=\frac{1}{2}AB=\frac{R\sqrt{3}}{2}\)
Xét \(\Delta OHA\) có:
\(\cos \widehat{OAH}=\frac{AH}{AO}=\frac{\sqrt{3}}{2}\)
\(\Rightarrow \widehat{OAH}={{30}^{0}}\Rightarrow \widehat{AOB}={{180}^{0}}-{{2.30}^{0}}={{120}^{0}}\)
\(\Rightarrow \widehat{xAB}=\frac{1}{2}\widehat{AOB}=\frac{1}{2}{{.120}^{0}}={{60}^{0}}\).
Chọn đáp án C.