Cho đường tròn ( O;R ), hai đường kính AB và CD vuông góc với nhau. E

Câu hỏi
Nhận biếtCho đường tròn \(\left( {O;\,\,R} \right),\) hai đường kính \(AB\) và \(CD\) vuông góc với nhau. \(E\) là điểm thuộc cung nhỏ \(BC\,\,\,\left( {E \ne B,\,\,C} \right),\) tiếp tuyến của đường tròn \(\left( {O;\,\,R} \right)\) tại \(E\) cắt đường thẳng \(AB\) tại \(I.\) Gọi \(F\) là giao điểm của \(DE\) và \(AB,\,\,K\) là điểm thuộc đường thẳng \(IE\) sao cho \(KF\) vuông góc với \(AB.\)
a) Chứng minh tứ giác \(OKEF\) nội tiếp.
b) Chứng minh \(\angle OKF = \angle ODF.\)
c) Chứng minh \(DE.DF = 2{R^2}.\)
d) Gọi \(M\) là giao điểm của \(OK\) với \(CF,\) tính \(\tan \angle MDC\) khi \(\angle EIB = {45^0}.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
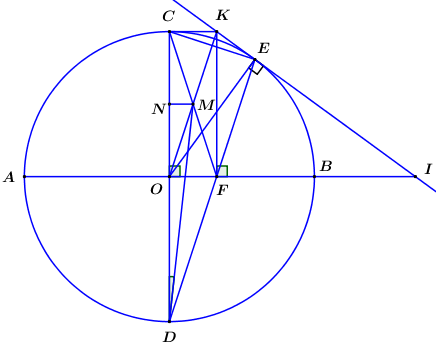
a. Chứng minh tứ giác \(OKEF\) nội tiếp.
Do \(EK\) là tiếp tuyến của \(\left( O \right) \Rightarrow \angle OEK = {90^0}\).
Lại có \(\angle OFK = {90^0}\,\,\left( {gt} \right) \Rightarrow \) Tứ giác \(OKEF\) có 2 đỉnh \(E,\,\,F\) kề nhau cùng nhìn \(OK\) dưới góc \({90^0}\).
\( \Rightarrow E,\,\,F\) thuộc đường tròn đường kính \(OK\) hay tứ giác \(OKEF\) nội tiếp.
b. Chứng minh \(\angle OKF = \angle ODF\).
Tứ giác \(OKEF\) nội tiếp (cmt) \( \Rightarrow \angle OKF = \angle OEF\) (hai góc nội tiếp cùng chắn cung \(OF\)).
Ta có \(OE = OD\,\,\left( { = R} \right) \Rightarrow \Delta ODE\) cân tại \(O \Rightarrow \angle OEF = \angle ODF\).
\( \Rightarrow \angle OKF = \angle ODF\,\,\left( { = \angle OKF} \right)\).
c. Chứng minh \(DE.DF = 2{R^2}\).
Nối \(CE\). Ta có \(\angle DEC = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tam giác \(DOF\) và tam giác \(DEC\) có :
\(\angle CDE\) chung;
\(\angle DOF = \angle DEC = {90^0}\) ;
\( \Rightarrow \Delta DOF \sim \Delta DEC\,\,\left( {g.g} \right) \Rightarrow \frac{{DO}}{{DE}} = \frac{{DF}}{{DC}} \Rightarrow DE.DF = DO.DC = R.2R = 2{R^2}\).
d. Gọi \(M\) là giao điểm của \(OK\) với \(CF\), tính \(\tan \angle MDC\) khi \(\angle EIB = {45^0}\).
Ta có \(AB\) là trung trực của \(CD\). Mà \(F \in AB \Rightarrow FC = FD \Rightarrow \Delta FCD\) cân tại \(F \Rightarrow \angle ODF = \angle OCF\).
Mà \(\angle OKF = \angle ODF\) (cmt) \( \Rightarrow \angle OCF = \angle OKF \Rightarrow \) Tứ giác \(OCKF\) là tứ giác nội tiếp (Tứ giác có 2 đỉnh kề nhau cùng nhìn 1 cạnh dưới các góc bằng nhau).
Mà tứ giác \(OKEF\) nội tiếp đường tròn đường kính \(OK\).
\( \Rightarrow O,\,\,C,\,\,K,\,\,E,\,\,F\) cùng thuộc đường tròn đường kinh \(OK \Rightarrow \angle OCK = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác \(OCKF\) có : \(\angle OCK = \angle COF = \angle OFK = {90^0} \Rightarrow \) Tứ giác \(OCKF\) là hình chữ nhật (Tứ giác có 3 góc vuông). Mà \(M = OK \cap CF \Rightarrow \) M là trung điểm của \(OK,\,\,CF\).
Gọi \(N\) là trung điểm của \(OC\) \( \Rightarrow MN\) là đường trung bình của tam giác \(OCF\)\( \Rightarrow MN = \frac{1}{2}OF\) và \(MN//OF \Rightarrow MN \bot OC\).
Xét tam giác vuông \(OEI\) có : \(\sin {45^0} = \frac{{OE}}{{OI}} \Rightarrow OI = \frac{{OE}}{{\sin {{45}^0}}} = \frac{R}{{\frac{{\sqrt 2 }}{2}}} = R\sqrt 2 \).
\(OCKF\) là hình chữ nhật \( \Rightarrow KF = OC = R\).
Xét tam giác vuông \(IKF\) có \(\angle EIB = \angle KIF = {45^0} \Rightarrow \Delta IKF\) vuông cân tại \(F \Rightarrow IF = KF = R\).
\( \Rightarrow OF = OI - IF = R\sqrt 2 - R = R\left( {\sqrt 2 - 1} \right)\).
\( \Rightarrow MN = \frac{1}{2}OF = \frac{{R\left( {\sqrt 2 - 1} \right)}}{2}\).
Ta có: \(DN = OD + ON = R + \frac{R}{2} = \frac{{3R}}{2}\).
Xét tam giác vuông \(DMN\) (\(MN \bot OC \Rightarrow MN \bot DN\)) có:
\(\tan \angle MDN = \frac{{MN}}{{DN}} = \frac{{\frac{{R\left( {\sqrt 2 - 1} \right)}}{2}}}{{\frac{{3R}}{2}}} = \frac{{\sqrt 2 - 1}}{3} = \tan \angle MDC\)
Vậy \(\tan \angle MDC = \frac{{\sqrt 2 - 1}}{3}\).

