Cho đường tròn (O;5cm) và một dây cung AB = 6cm của ( O ). Khoảng cách

Câu hỏi
Nhận biếtCho đường tròn \((O;5cm) \) và một dây cung \(AB = 6cm \) của \( \left( O \right). \) Khoảng cách từ điểm \(O \) đến đường thẳng \(AB \) bằng
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
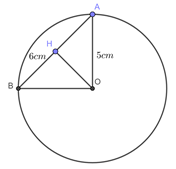
Gọi \(H\) là hình chiếu vuông góc của \(O\) xuống \(AB \Rightarrow d\left( {O;\,\,AB} \right) = OH.\)
\( \Rightarrow H\)là trung điểm của \(AB\) (mối liên hệ giữa đường kính và dây cung)
\( \Rightarrow AH = BH = \frac{{AB}}{2} = \frac{6}{2} = 3\,\,cm\)
Xét tam giác vuông \(AHO\) có \(O{A^2} = O{H^2} + A{H^2} \Leftrightarrow {5^2} = O{H^2} + {3^2} \Rightarrow OH = 4\)
Chọn A.

