Cho đường tròn ( O ), từ điểm A ngoài đường tròn vẽ đường thẳng AO cắt
Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right),\) từ điểm \(A\) ngoài đường tròn vẽ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,\;\;C\;\left( {AB < AC} \right).\) Qua \(A\) vẽ đường thẳng không đi qua \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,\;E\;\;\left( {AD < AE} \right).\) Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F.\)
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right).\) Chứng minh \(DM \bot AC.\)
c) Chứng minh \(CE.CF + AD.AE = A{C^2}.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
Cho đường tròn \(\left( O \right),\) từ điểm \(A\) ngoài đường tròn vẽ đường thẳng \(AO\) cắt đường tròn \(\left( O \right)\) tại \(B,\;\;C\;\left( {AB < AC} \right).\) Qua \(A\) vẽ đường thẳng không đi qua \(O\) cắt đường tròn \(\left( O \right)\) tại \(D,\;E\;\;\left( {AD < AE} \right).\) Đường thẳng vuông góc với \(AB\) tại \(A\) cắt đường thẳng \(CE\) tại \(F.\)
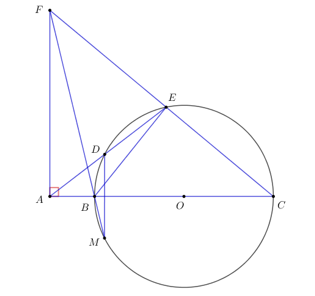
a) Chứng minh tứ giác \(ABEF\) nội tiếp.
Xét đường tròn \(\left( O \right)\) ta có: \(\widehat {BEC} = {90^0}\) (góc nội tiếp chắn nửa đường tròn).
Xét tứ giác \(ABEF\) ta có: \(\widehat {FAB} + \widehat {BEF} = {90^0} + {90^0} = {180^0}.\)
\( \Rightarrow ABEF\) là tứ giác nội tiếp. (tứ giác có tổng hai góc đối diện bằng \({180^0}\)).
b) Gọi \(M\) là giao điểm thứ hai của \(FB\) với đường tròn \(\left( O \right).\) Chứng minh \(DM \bot AC.\)
Vì tứ giác ABEF là tứ giác nội tiếp (cmt) \( \Rightarrow \widehat {AEB} = \widehat {AFB}\) (hai góc nội tiếp cùng chắn cung AB).
Lại có \(\widehat {AEB} = \widehat {BMD}\) (hai góc nội tiếp cùng chắn cung BD của đường tròn (O))
\( \Rightarrow \widehat {AFB} = \widehat {BMD}\). Mà hai góc này ở vị trí so le trong \( \Rightarrow AF//DM\).
Mà \(AF \bot AC \Rightarrow DM \bot AC\).
c) Chứng minh \(CE.CF + AD.AE = A{C^2}.\)
Xét tam giác ACD và tam giác ABE có
\(\widehat {CAE}\) chung;
\(\widehat {ACD} = \widehat {AEB}\) (hai góc nội tiếp cùng chắn cung BD)
\( \Rightarrow \Delta ACD \sim \Delta AEB\,\left( {g.g} \right) \Rightarrow \frac{{AC}}{{AE}} = \frac{{AD}}{{AB}} \Rightarrow AD.AE = AC.AB\,\,\left( 1 \right)\)
Xét tam giác CBE và tam giác CFA có:
\(\widehat {ACB}\) chung;
\(\widehat {CEB} = \widehat {CAF} = {90^0}\)
\( \Rightarrow \Delta CBE \sim \Delta CFA\,\,\left( {g.g} \right) \Rightarrow \frac{{CE}}{{CA}} = \frac{{CB}}{{CF}} \Rightarrow CE.CF = CA.CB\,\,\left( 2 \right)\)
Từ (1) và (2) \( \Rightarrow CE.CF + AD.AE = CA.CB + AC.AB = AC\left( {AB + BC} \right) = A{C^2}\,\,\left( {dpcm} \right)\)
