Cho đường tròn ( O ) đường kính AB và điểm C thuộc đường tròn ( O )(C

Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\) đường kính AB và điểm C thuộc đường tròn \(\left( O \right)\)(C khác A và B) sao cho\(AC > BC\). Qua O vẽ đường thẳng vuông góc với dây cung AC tại H. Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt OH tại D. Đoạn thẳng DB cắt đường tròn \(\left( O \right)\) tại E.
a) Chứng minh \(HA = HC,\angle DCO = {90^o}\)
b) Chứng minh rằng \(DH.DO = DE.DB\)
c) Trên tia đối của tia EA lấy điểm F sao cho E là trung điểm cạnh AF. Từ F vẽ đường thẳng vuông góc với đường thẳng AD tại K. Đoạn thẳng FK cắt đường thẳng BC tại M. Chứng minh\(MK = MF\).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
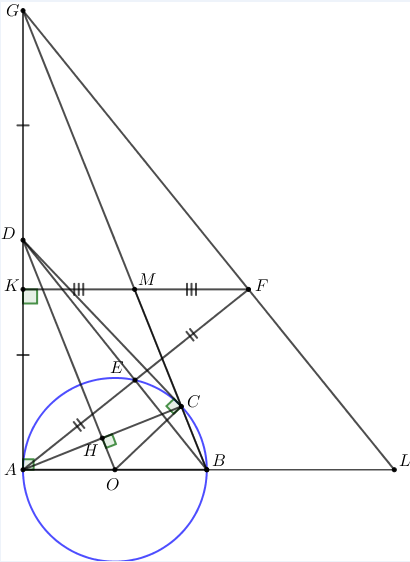
a) Chứng minh \(HA = HC,\angle DCO = {90^o}\)
Xét tam giác AOC có: \(AO = CO\)(do cùng là bán kính), suy ra tam giác AOC cân tại O
Mà có OH là đường cao ứng với đỉnh O nên OH đồng thời cũng là trung trực của AC
Suy ra \(HA = HC\). (đpcm)
Xét tam giác AOC cân tại O có OH là đường cao, suy ra OH đồng thời là đường phân giác
\( \Rightarrow \angle AOH = \angle COH\).
Xét tam giác DOC và tam giác DOA có:
+) Chung cạnh OD
+) \(AO = CO\)(do cùng là bán kính)
+) \(\angle AOH = \angle COH\)
\( \Rightarrow \Delta DOC = \Delta DOA \Rightarrow \angle DCO = \angle DAO = {90^o}\)(do AD là tiếp tuyến nên \(\angle DAO = {90^o}\))\(\) \(\)
b) Chứng minh rằng \(DH.DO = DE.DB\)
Xét tam giác vuông ADO vuông tại A có AH là đường cao
\( \Rightarrow A{D^2} = DH.DO\) (hệ thức lượng trong tam giác vuông) (1)
Xét tam giác vuông DAB vuông tại A có AE là đường cao ( AE vuông góc với BD do \(\angle AEB\)là góc nội tiếp chắn nửa đường tròn)
\( \Rightarrow A{D^2} = DE.DB\) (hệ thức lượng trong tam giác vuông) (2)
Từ (1) và (2) suy ra \(DH.DO = DE.DB\;\;\left( { = A{D^2}} \right)\) (đpcm) \(\) \(\)
c) Trên tia đối của tia EA lấy điểm F sao cho E là trung điểm cạnh AF. Từ F vẽ đường thẳng vuông góc với đường thẳng AD tại K. Đoạn thẳng FK cắt đường thẳng BC tại M. Chứng minh\(MK = MF\).
Kéo dài BM cắt AD tại G, GF cắt AB tại L
Xét tam giác ABG có:
\(\begin{array}{l}DO//BG\;\left( { \bot AC} \right)\\OA = OB\;\left( { = R} \right)\end{array}\)
\( \Rightarrow AD = DG\) (tính chất đường trung bình)
Xét tam giác GFA có:
+) D là trung điểm của AG (do\(AD = DG\))
+) E là trung điểm của AF (giả thiết)
\( \Rightarrow \) DE song song với GF (tính chất đường trung bình)
Xét tam giác GAL có:
+) D là trung điểm AG (do \(AD = DG\))
+) DB song song với GL (do DE song song với GF)
Suy ra B là trung điểm của AL (tính chất đường trung bình), suy ra\(AB = \frac{1}{2}AL\)\(\)
Xét tam giác GKM có KM song song với AB (do cùng vuông góc với AG)
\( \Rightarrow \frac{{KM}}{{AB}} = \frac{{KG}}{{AG}}\) (định lí Ta-lét) (3)
Xét tam giác GAL có KF song song với AL (do cùng vuông góc với AG)
\( \Rightarrow \frac{{KF}}{{AL}} = \frac{{GK}}{{AG}}\) (định lí Ta-lét) (4)
Từ (3) và (4) \( \Rightarrow \frac{{KM}}{{AB}} = \frac{{KF}}{{AL}}\). Mà có \(AB = \frac{1}{2}AL\) (cmt)
\( \Rightarrow KM = \frac{1}{2}KF \Rightarrow MF = KF - KM = KF - \frac{1}{2}KF = \frac{1}{2}KF \Rightarrow KF = KM\)(đpcm).

