Cho đường tròn ( O ) đường kính AB = 6cm. Gọi H là điểm thuộc đoạn thẳ

Câu hỏi
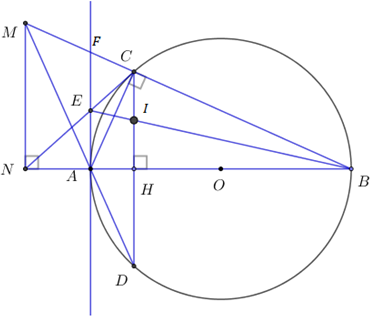
Nhận biếtCho đường tròn \(\left( O \right)\) đường kính \(AB = 6cm.\) Gọi \(H\) là điểm thuộc đoạn thẳng \(AB\) sao cho \(AH = 1cm.\) Qua \(H\) vẽ đường thẳng vuông góc với \(AB,\) đường thẳng này cắt đường tròn \(\left( O \right)\) tại C và D. Hai đường thẳng BC và AD cắt nhau tại M. Gọi N là hình chiếu của M trên đường thẳng AB.
a) Chứng minh tứ giác MNAC nội tiếp.
b) Tính độ dài CH và \(\tan \angle ABC\)
c) Chứng minh NC là tiếp tuyến của đường tròn \(\left( O \right)\).
d) Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt NC tại E. Chứng minh đường thẳng EB đi qua trung điểm của đoạn thẳng CH.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Chứng minh tứ giác MNAC nội tiếp.
Do \(\angle ACB\) là góc nội tiếp chắn nửa đường tròn nên \(\angle ACB = {90^0} \Rightarrow \angle ACM = {90^0}\).
Xét tứ giác \(MNAC\) có \(\angle ACM + \angle ANM = {90^0} + {90^0} = {180^0}\)
\( \Rightarrow \) Tứ giác \(MNAC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800).’
b) Tính độ dài CH và \(\tan \angle ABC\)
Ta có: \(BH = AB - AH = 6 - 1 = 5\,\,\left( {cm} \right)\)
Áp dụng hệ thức lượng trong tam giác vuông ABC có: \(A{H^2} = HA.HB = 1.5 = 5 \Rightarrow AH = \sqrt 5 \,\,\left( {cm} \right)\)
\( \Rightarrow \tan \angle ABC = \frac{{HA}}{{HB}} = \frac{{\sqrt 5 }}{5} = \frac{1}{{\sqrt 5 }}\)
c) Chứng minh NC là tiếp tuyến của đường tròn \(\left( O \right)\).
Ta có \(MN \bot AB;\,\,CH \bot AB \Rightarrow MN//CH\)
\( \Rightarrow \angle AMN = \angle ADC\) (so le trong)
Mà \(\angle AMN = \angle ACN\) (hai góc nội tiếp cùng chắn cung AN) \( \Rightarrow \angle ACN = \angle ADC\).
Mà \(\angle ADC\) nội tiếp chắn cung AC, \(\angle ACN\) ở vị trí góc tạo bởi tiếp tuyến và dây cung chắn cung AC.
\( \Rightarrow CN\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại C.
d) Tiếp tuyến tại A của đường tròn \(\left( O \right)\) cắt NC tại E. Chứng minh đường thẳng EB đi qua trung điểm của đoạn thẳng CH.
Kéo dài AE cắt BM tại F.
Ta có \(EA = EC\,\,\left( 1 \right)\) (tính chất hai tiếp tuyến cắt nhau) \( \Rightarrow \Delta EAC\) cân tại E \( \Rightarrow \angle EAC = \angle ECA\)
\( \Rightarrow {90^0} - \angle EAC = {90^0} - \angle ECA \Leftrightarrow \angle EFC = \angle ECF \Rightarrow \Delta EFC\) cân tại E \( \Rightarrow EC = EF\) (2)
Từ (1) và (2) \( \Rightarrow EA = EC = EF\)
Ta có \(AF \bot AB\,\left( {gt} \right);\,\,CH \bot AB\,\,\left( {gt} \right) \Rightarrow AF//CH\)
Gọi \(I = BE \cap AF\), áp dụng định lí Ta-let ta có: \(\frac{{HI}}{{AE}} = \frac{{BI}}{{BE}};\,\,\frac{{CI}}{{EF}} = \frac{{BI}}{{BE}} \Rightarrow \frac{{HI}}{{AE}} = \frac{{CI}}{{EF}}\).
Mà \(AE = EF\,\,\left( {cmt} \right) \Rightarrow HI = CI \Rightarrow I\) là trung điểm của HC. (đpcm)

