Cho đường tròn ( O )đường kính AB = 5cm. Lấy điểm C thuộc đường tròn

Câu hỏi
Nhận biếtCho đường tròn \(\left( O \right)\)đường kính \(AB = 5\,cm\). Lấy điểm \(C\) thuộc đường tròn \(\left( O \right)\)sao cho \(AC = 4\,cm\). Gọi \(M\) là trung điểm của đoạn \(AC.\) Tiếp tuyến của đường tròn \(\left( O \right)\)tại \(C\) cắt tia \(OM\) tại \(P.\)
1) So sánh độ dài hai đoạn thẳng \(AB,\,\,BC\) và giải thích.
2) Chứng minh rằng \(CA \bot CB\).
3) Chứng minh rằng \(PA\) là tiếp tuyến của đường tròn \(\left( O \right)\)
4) Vẽ \(CH\) vuông góc với \(AB,\) \(H \in AB\) và \(BQ\) vuông góc với \(CP,\) \(Q \in CP\). Tính \(CQ.\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
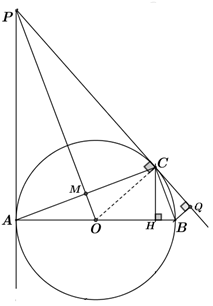
1) So sánh độ dài hai đoạn thẳng \(AB,\,\,BC\) và giải thích.
Cách 1:
Ta có: \(C\) nằm trên đường tròn \(\left( O \right)\)đường kính \(AB = 5\,cm;\,\,AC = 4cm\) \( \Rightarrow AC < AB\)
Suy ra \(AC\) không thể là đường kính của đường tròn \(\left( O \right)\)\( \Rightarrow BC\) không thể là đường kính của đường tròn \(\left( O \right)\)
\( \Rightarrow BC < 2r\,\,\,\,hay\,\,\,\,BC < AB\)
Vậy \(\,BC < AB\).
Cách 2:
Ta có: \(\Delta ABC\) là tam giác nội tiếp đường tròn \(\left( O \right),\) đường kính \(AB.\)
\( \Rightarrow \Delta ABC\) vuông tại \(C.\)
\( \Rightarrow BC < AB\) (cạnh góc vuông nhỏ hơn cạnh huyền).
2) Chứng minh rằng \(CA \bot CB\).
Ta có: \(\Delta ABC\) vuông tại \(C\) (cm a))
\( \Rightarrow AC \bot BC = \left\{ C \right\}.\) (đpcm)
3) Chứng minh rằng \(PA\) là tiếp tuyến của đường tròn \(\left( O \right)\)
Xét \(\Delta OAC\)cân tại \(O\) có \(M\) là trung điểm của \(AC\,\,\left( {gt} \right)\)
\( \Rightarrow OM\)là đường trung tuyến đồng thời là đường phân giác của \(\angle AOC\) (tính chất).
\( \Rightarrow \)\(\angle AOM = \angle COM\) hay \(\angle AOP = \angle COP\)
Xét \(\Delta AOP\) và \(\Delta COP\) có:
\(\begin{array}{l}\,AO = CO\,\,\,\left( { = r} \right)\\\angle AOP = \angle COP\,\,\,\left( {cmt} \right)\\\,OP\,\,\,chung\\ \Rightarrow \Delta AOP = \Delta COP\,\,\,\,\left( {c - g - c} \right)\end{array}\)
\( \Rightarrow \angle PAO = \angle PCO = {90^0}\) (do \(PC\) là tiếp tuyến của đường tròn \(\left( O \right)\)tại \(C\)).
\( \Rightarrow PA \bot OA\)
\( \Rightarrow PA\) là tiếp tuyến của đường tròn \(\left( O \right)\) tại \(A.\) (đpcm)
4) Vẽ \(CH\) vuông góc với \(AB,\) \(H \in AB\) và \(BQ\) vuông góc với \(CP,\) \(Q \in CP\). Tính \(CQ.\)
Ta có: \(\left\{ \begin{array}{l}BC \bot AC\left( {cmt} \right)\\OP \bot AC\left( {cmt} \right)\end{array} \right. \Rightarrow BC\parallel OP\) (từ vuông góc đến song song).
\( \Rightarrow \left\{ \begin{array}{l}\angle CBH = \angle POA\\\angle QCB = \angle CPO\end{array} \right.\) (các góc đồng vị) (1)
Lại có: \(\Delta AOP = \Delta COP\,\left( {cmt} \right) \Rightarrow \angle APO = \angle CPO = \angle QCB\,\,\,\,\left( 2 \right)\)
Mà :\(\angle APO + \angle POA = {90^0}\) (\(\Delta POA\) vuông tại \(A\)) (3)
Từ (1), (2), (3) \( \Rightarrow \angle CBH + \angle QCB = {90^0}\)
\(\Delta CHB\) vuông tại \(H\) \( \Rightarrow \angle CBH + \angle HCB = {90^0}\)
\( \Rightarrow \angle HCB = \angle QCB\) (cùng phụ với \(\angle CBH\))
Xét \(\Delta HCB\) và \(\Delta QCB\) có:
\(\begin{array}{l}\angle HCB = \angle QCB\\BC\,chung\\\angle CBH = \angle CBQ\\ \Rightarrow \Delta HCB = \Delta QCB\,\,\,\,\left( {g - c - g} \right)\end{array}\)
\( \Rightarrow CQ = CH\) (hai cạnh tương ứng).
Trong \(\Delta ABC\,\)vuông tại \(C\) có: \(B{C^2} = A{B^2} - A{C^2} = {5^2} - {4^2} = 9\)
Áp dụng hệ thức lượng trong tam giác vuông ABC ta có:
\(\begin{array}{l}\frac{1}{{C{H^2}}} = \frac{1}{{C{A^2}}} + \frac{1}{{C{B^2}}} = \frac{1}{{{4^2}}} + \frac{1}{9} = \frac{{25}}{{144}}\\ \Rightarrow C{H^2} = \frac{{144}}{{25}} \Rightarrow CH = \sqrt {\frac{{144}}{{25}}} = 2,4\,\,\,\,\left( {cm} \right).\\ \Rightarrow CQ = 2,4\,\,\,\left( {cm} \right).\end{array}\)
Vậy \(CQ = 2,4\,\,\,cm.\)

