Cho đường tròn ( O ) đi qua hai đỉnh AB và tiếp xúc với cạnh CD của một hình vuông (tham khảo hình v

Câu hỏi
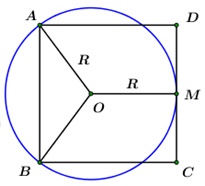
Nhận biếtCho đường tròn \(\left( O \right)\) đi qua hai đỉnh \(A,\,\,B\) và tiếp xúc với cạnh \(CD\) của một hình vuông (tham khảo hình vẽ). Tính bán kính \(R\) của đường tròn đó biết cạnh hình vuông dài \(8cm.\)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
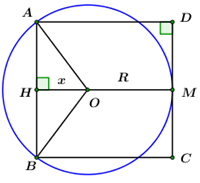
Gọi \(H\) là trung điểm của \(AB \Rightarrow OH \bot AB = \left\{ H \right\}\) (mối liên hệ giữa đường kính và dây cung).
\( \Rightarrow \left\{ \begin{array}{l}AH = AB\\MH = OM + OH\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}AH = BH = 4\\8 = R + OH\end{array} \right..\)
Đặt \(OH = x\,\,\left( {0 < x < 8} \right) \Rightarrow x = OH = 8 - R.\)
Áp dụng định lý Pitago cho \(\Delta AOH\) vuông tại \(H\) ta có:
\(\begin{array}{l}O{H^2} = A{O^2} - A{H^2} \Leftrightarrow {\left( {8 - R} \right)^2} = {R^2} - {4^2}\\ \Leftrightarrow 64 - 16R + {R^2} = {R^2} - 16\\ \Leftrightarrow 16R = 80 \Leftrightarrow R = 5\,\,cm.\end{array}\)
Chọn D.