Cho đường thẳng ( d1 ) :y = ( m - 1 )x + 2m + 1 a) Tìm m để đường thẳng d1 cắt trục tung tại điểm

Câu hỏi
Nhận biếtCho đường thẳng \(\left( {{d_1}} \right) :y = \left( {m - 1} \right)x + 2m + 1\)
a) Tìm \(m\) để đường thẳng \({{d}_{1}}\) cắt trục tung tại điểm có tung độ là \(-3\) Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng \(\left( d \right):y=x+1\) nằm trên trục hoành.
b) Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \({{d}_{1}}\) đạt giá trị lớn nhất.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a) Tìm \(m\) để đường thẳng \({{d}_{1}}\) cắt trục tung tại điểm có tung độ là \(-3\) Vẽ đồ thị hàm số vừa tìm được và chứng tỏ giao điểm của đồ thị hàm số vừa tìm được với đường thẳng \(\left( d \right):y=x+1\) nằm trên trục hoành.
Vì \({{d}_{1}}\) cắt trục tung tại điểm có tung độ là \(-3\) suy ra \(\left( 0;-3 \right)\) nằm trên đường thẳng \({{d}_{1}}\)
\(\Rightarrow -3=\left( m-1 \right).0+2m+1\Leftrightarrow 2m=-4\Leftrightarrow m=-2\)
Với \(m=-2\) ta có phương trình đường thẳng \(\left( {{d}_{1}} \right):y=-3x-3\)
Nhận thấy: \(A\left( 0;-3 \right),\ B\left( -1;\ 0 \right)\) nằm trên đồ thị hàm số. Vì hàm số \(\left( {{d}_{1}} \right):y=-3x-3\) là hàm số bậc nhất nên đồ thị của nó có dạng đường thẳng, từ đó ta có đồ thị:
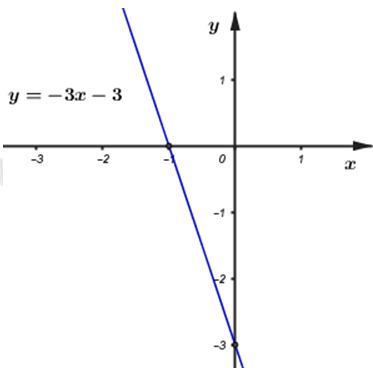
Hoành độ giao điểm của \(\left( {{d}_{1}} \right):y=-3x-3\) và \(\left( d \right):y=x+1\) là nghiệm của phương trình:
\(x+1=-3x-3\Leftrightarrow 4x=-4\Leftrightarrow x=-1\Rightarrow y=x+1=-1+1=0\)
Vậy giao điểm của \(\left( {{d}_{1}} \right):y=-3x-3\) và \(\left( d \right):y=x+1\) là \(\left( -1;0 \right)\) Nhận thấy điểm \(\left( -1;0 \right)\) nằm trên trục hoành (do có tung độ bằng 0).
Vậy ta có điều cần chứng minh
b) Tìm \(m\) để khoảng cách từ gốc tọa độ đến đường thẳng \({{d}_{1}}\) đạt giá trị lớn nhất.
+) Với \(x=0\Rightarrow y=2m+1\Rightarrow A\left( 0;2m+1 \right)\) là giao điểm của \({{d}_{1}}\) với trục tung\(\Rightarrow OA=\left| 2m+1 \right|\)
+) Với \(y=0\Rightarrow x=\frac{-\left( 2m+1 \right)}{m-1}\Rightarrow B\left( \frac{-\left( 2m+1 \right)}{m-1};0 \right)\) là giao điểm của \({{d}_{1}}\) với trục hoành
\(\Rightarrow OB=\left| \frac{-\left( 2m+1 \right)}{m-1} \right|\)
Từ O kẻ đường cao OH với, ta được OH chính là khoảng cách từ O tới \({{d}_{1}}\)
Xét tam giác vuông OAB vuông tại O có đường cao OH
\(\Rightarrow \frac{1}{O{{H}^{2}}}=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}\) (hệ thức lượng trong tam giác vuông)
Đặt \(\frac{1}{O{{H}^{2}}}=t\) ta có:
\(\begin{align} & t=\frac{1}{O{{A}^{2}}}+\frac{1}{O{{B}^{2}}}=\frac{1}{{{\left( 2m+1 \right)}^{2}}}+\frac{{{\left( m-1 \right)}^{2}}}{{{\left( 2m+1 \right)}^{2}}}=\frac{{{m}^{2}}-2m+2}{4{{m}^{2}}+4m+1}\ \ \ \left( m\ne -\frac{1}{2} \right) \\ & \Leftrightarrow 4{{m}^{2}}t+4mt+t={{m}^{2}}-2m+2 \\ & \Rightarrow {{m}^{2}}\left( 4t-1 \right)+2m\left( 2t+1 \right)+t-2=0 \\ \end{align}\)
Coi đây là phương trình bậc 2 ẩn \(m\) phương trình có nghiệm khi \(\) \(\) \(\)
\(\begin{align} & \Delta '={{\left( 2t+1 \right)}^{2}}-\left( 4t-1 \right)\left( t-2 \right)\ge 0 \\ & \Leftrightarrow 4{{t}^{2}}+4t+1-4{{t}^{2}}+9t-2\ge 0 \\ & \Leftrightarrow 13t-1\ge 0\Leftrightarrow t\ge \frac{1}{13} \\ & \Rightarrow \frac{1}{O{{H}^{2}}}\ge \frac{1}{13}\Rightarrow OH\le \sqrt{13} \\ \end{align}\)
Dấu “=” xảy ra khi phương trình có nghiệm kép \(\)
\(\Leftrightarrow m=\frac{-b}{2a}=\frac{-\left( 4t+2 \right)}{2\left( 4t-1 \right)}=-\frac{\frac{4}{13}+2}{2.\left( \frac{4}{13}-1 \right)}=\frac{5}{3}\ \ \ \left( tm \right)\)
Vậy \(m=\frac{5}{3}\) là giá trị cần tìm.
Chọn D

