Cho đường thẳng ( d1 ):y = 2x + 2. a) Vẽ đường thẳng ( d1 ) trên mặt

Câu hỏi
Nhận biếtCho đường thẳng \( \left( {{d_1}} \right):y = 2x + 2. \)
a) Vẽ đường thẳng \( \left( {{d_1}} \right) \) trên mặt phẳng tọa độ \(Oxy. \)
b) Tìm tọa độ giao điểm của \( \left( {{d_1}} \right) \) và \( \left( {{d_2}} \right):y = x - 3. \)
c) Cho đường thẳng \( \left( {{d_3}} \right):y = mx + 5. \) Tìm giá trị của \(m \) để ba đường thẳng \( \left( {{d_1}} \right), \, \left( {{d_2}} \right), \, \left( {{d_3}} \right) \) cắt nhau tại một điểm.
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Cho đường thẳng \(\left( {{d_1}} \right):y = 2x + 2\)
a) Vẽ đường thẳng \(\left( {{d_1}} \right)\) trên mặt phẳng tọa độ \(Oxy.\)
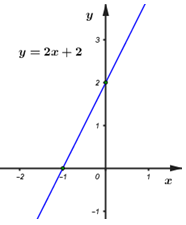
Cho \(x = 0 \Rightarrow y = 2\)
\(y = 0 \Rightarrow x = - 1\)
Đồ thị hàm số \(y = 2x + 2\) là đường thẳng đi qua hai điểm có tọa độ \(\left( {0;2} \right)\)và \(\left( { - 1;0} \right)\)
b) Tìm tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right):y = x - 3.\)
Xét phương trình hoành độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,2x + 2 = x - 3\\ \Leftrightarrow 2x - x = - 3 - 2\\ \Leftrightarrow x = - 5\end{array}\)
Thay \(x = - 5\) vào hàm số \(y = x - 3\) ta được \(y = - 5 - 3 = - 8\)
Vậy tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(\left( { - 5; - 8} \right)\).
c) Cho đường thẳng \(\left( {{d_3}} \right):y = mx + 5.\) Tìm giá trị của \(m\) để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\,\left( {{d_3}} \right)\) cắt nhau tại một điểm.
Để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) cắt nhau thì \(m \ne \left\{ {1;2} \right\}\)
Theo câu b) ta có tọa độ giao điểm của \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) là \(\left( { - 5; - 8} \right)\).
Để ba đường thẳng \(\left( {{d_1}} \right),\left( {{d_2}} \right),\left( {{d_3}} \right)\) đồng quy thì điểm có tọa độ \(\left( { - 5; - 8} \right)\) cũng thuộc đường thẳng \(\left( {{d_3}} \right).\)
Thay \(x = - 5;y = - 8\) vào hàm số \(y = mx + 5\) ta được: \( - 8 = m\left( { - 5} \right) + 5 \Leftrightarrow m = \frac{{13}}{5}\) (thỏa mãn)
Vậy \(m = \frac{{13}}{5}.\)
Chọn B.

