Cho điểm M thuộc nửa đường tròn ( O;R ), đường kính AB (M khác A và B)

Lời giải của Tự Học 365

Giải chi tiết:

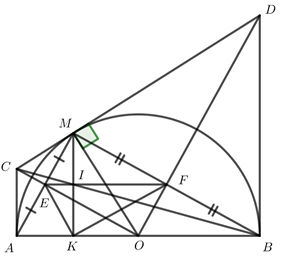
1. Chứng minh rằng: Tứ giác MEOF là hình chữ nhật.

Do \(\Delta MAB\) nội tiếp nửa đường tròn \(\left( O \right)\) có cạnh AB là đường kính

\( \Rightarrow \Delta MAB\)  vuông tại M \( \Rightarrow \angle AMB = {90^o}\) hay \(\angle EMF = {90^o}\)

+) Xét nửa đường tròn \(\left( O \right)\) có E là trung điểm của MA (gt)

\( \Rightarrow OE \bot MA\) (quan hệ vuông góc giữa đường kính và dây cung)

\( \Rightarrow \angle MEO = {90^o}\)

Tương tự ta cũng được: \(\angle MFO = {90^o}\)

+) Xét tứ giác MEOF có \(\angle EMF = \angle MEO = \angle MFO = {90^o}\;\;\left( {cmt} \right)\)

\( \Rightarrow \) Tứ giác MEOF là hình chữ nhật (dhnb).

2. Tiếp tuyến tại M của nửa đường tròn \(\left( {O;R} \right)\) cắt các đường thẳng OE và OF lần lượt tại C và D. Chứng minh: CA tiếp xúc với nửa đường tròn \(\left( {O;R} \right)\). Tính độ dài đoạn thẳng CA khi \(R = 3cm\) và \(\angle MAO = {30^o}\).

Ta có: \(OM = OA = R\) (A, M thuộc nửa đường tròn \(\left( O \right)\)) ;

\(EM = EA\) (E là trung điểm của MA)

\( \Rightarrow \) OE là đường trung trực của MA hay OC là đường trung trực của MA. (tính chất đường trung trực)

\( \Rightarrow CA = CM\) (tính chất đường trung trực)

+) Xét \(\Delta ACO\) và \(\Delta MCO\) có:

\(\begin{array}{l}CA = CM\;\;\left( {cmt} \right)\\CO\;chung\\OA = OM\;\;\left( { = R} \right)\\ \Rightarrow \Delta ACO = \Delta MCO\;\;\left( {c - c - c} \right).\end{array}\)

\( \Rightarrow \angle CAO = \angle CMO = {90^o}\) (2 góc tương ứng)

\( \Rightarrow CA \bot AB\) mà \(A \in \left( O \right)\)

\( \Rightarrow \) CA là tiếp tuyến của nửa đường tròn \(\left( {O;R} \right)\) hay CA tiếp xúc với nửa đường tròn \(\left( {O;R} \right)\).

+) Xét \(\Delta AEO\) vuông tại E có \(\angle EAO = {30^o} \Rightarrow \angle AOE = {90^0} - \angle EAO = {60^o}\) (tổng 3 góc trong tam giác)

Hay \(\angle AOC = {60^o}\)

Xét tam giác OAC vuông tại \(A\;\;\left( {CA \bot AB} \right)\) ta có:

\(\tan \angle AOC = \frac{{CA}}{{OA}} \Rightarrow CA = OA.\tan \angle AOC = 3\sqrt 3 \;\;\left( {cm} \right)\)

3. Chứng minh: \(AC.BD = {R^2}\) và \({S_{ACDB}} \ge 2{R^2}\).

Ta có: \(OM = OB = R\) (B, M thuộc nửa đường tròn \(\left( O \right)\)) ;

\(FM = FB\) (F là trung điểm của MB)

\( \Rightarrow \) OF là đường trung trực của MB hay OD là đường trung trực của MB. (tính chất đường trung trực)

\( \Rightarrow DB = DM\) (tính chất đường trung trực)

Ta có tứ giác \(MEOF\) là hình chữ nhật (cm a))

\( \Rightarrow \angle EOF = {90^0}\;\;hay\;\;\angle COD = {90^0}.\)

Theo đề bài ta có: \(CD\) là tiếp tuyến của \(\left( {O;\;R} \right)\) tại \(M \Rightarrow OM \bot CD.\) (tính chất tiếp tuyến)

Áp dụng hệ thức lượng trong \(\Delta OCD\) vuông tại\(O,\) có đường cao \(OM\)  ta có:

\(O{M^2} = CM.DM = {R^2}.\)

Lại có: \(DM = DB\;\;\left( {cmt} \right),\;\;CA = CM\;\;\left( {cmt} \right)\)

\( \Rightarrow CA.BD = CM.DM = {R^2}\;\;\;\left( {dpcm} \right)\)

+) Xét \(\Delta DMO\) và \(\Delta DBO\) có:

\(\begin{array}{l}DM = DB\;\;\left( {cmt} \right)\\DO\;chung\\OM = OB\;\;\left( { = R} \right)\\ \Rightarrow \Delta DMO = \Delta DBO\;\;\left( {c - c - c} \right).\end{array}\)

\( \Rightarrow \angle DMO = \angle DBO = {90^o}\) (2 góc tương ứng)

\( \Rightarrow DB \bot AB\) mà \(B \in \left( O \right)\)

Lại có: \(AC \bot AB\;\;\left( {cmt} \right)\)

\( \Rightarrow CA//BD\;\;\left( { \bot AB} \right)\) (từ vuông góc đến song song)

\( \Rightarrow CABD\) là hình thang vuông tại \(A,\;B.\)

\( \Rightarrow {S_{ACDB}} = \frac{1}{2}\left( {AC + BD} \right).AB\)

Áp dụng bất đẳng thức Cô-si ta được:

\(AC + BD \ge 2\sqrt {AC.BD}  = 2\sqrt {{R^2}}  = 2R\)

\( \Rightarrow {S_{ACDB}} = \frac{1}{2}\left( {AC + BD} \right).AB \ge \frac{1}{2}.2R.2R = 2{R^2}\)   

Vậy \({S_{ACDB}} \ge 2{R^2}\;\;\left( {dpcm} \right).\)

4. Gọi I là giao điểm của BC và EF, MI cắt AB tại K. Chứng minh rằng: EF là đường trung trực của MK.

Ta có: \(EOFM\) là hình chữ nhật (cmt) \( \Rightarrow \left\{ \begin{array}{l}ME//OF;\;EO//MF\\ME = OF;\;EO = MF\end{array} \right.\)  (tính chất hình chữ nhật).

\(\Delta CEI\) và \(\Delta BFI\) có: \(CE//BF \Rightarrow \frac{{CI}}{{IB}} = \frac{{CE}}{{BF}}\) (Hệ quả định lý Ta-lét)   (1)

\(\Delta COD\) có \(ME//OD \Rightarrow \frac{{CE}}{{EO}} = \frac{{CM}}{{MD}}\) (Định lý Ta-lét)

Mà \(EO = MF = BF \Rightarrow \frac{{CE}}{{BF}} = \frac{{CM}}{{MD}} = \frac{{CE}}{{EO}}\) (2)

Từ (1) và (2) \( \Rightarrow \frac{{CI}}{{IB}} = \frac{{CM}}{{MD}}\)

\( \Rightarrow MI//BD\) (Định lý Ta-lét đảo) hay \(MK//BD\) mà \(BD \bot AB\;\left( {cmt} \right)\)

\( \Rightarrow MK \bot AB\)

Xét tam giác AKM vuông tại  \(K\;\;\left( {MK \bot AB} \right)\) có KE là đường trung tuyến

\( \Rightarrow EM = EK\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

Xét tam giác MKB vuông tại  \(K\;\;\left( {MK \bot AB} \right)\) có KF là đường trung tuyến

\( \Rightarrow FM = FK\) (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

\( \Rightarrow \) EF là đường trung trực của MK  (đpcm).