Cho điểm E thuộc nửa đường tròn tâm O, đường kính MN. Kẻ tiếp tuyến tạ

Câu hỏi
Nhận biếtCho điểm E thuộc nửa đường tròn tâm O, đường kính MN. Kẻ tiếp tuyến tại N của nửa đường tròn tâm O, tiếp tuyến này cắt đường thẳng ME tại D.
1) Chứng minh rằng: \(\Delta MEN\) vuông tại E. Từ đó chứng minh \(DE.DM = D{N^2}\)
2) Từ O kẻ OI vuông góc với ME (\(I \in ME\)).
Chứng minh rẳng: 4 điểm O; I; D; N cùng thuộc một đường tròn.
3) Vẽ đường tròn đường kính OD, cắt nửa đường tròn tâm O tại điểm thứ hai là A. Chứng minh rằng: DA là tiếp tuyến của nửa đường tròn tâm O.
4) Chứng minh rằng: \(\angle DEA = \angle DAM\)
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
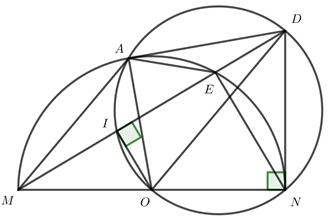
1) Chứng minh rằng: \(\Delta MEN\) vuông tại E. Từ đó chứng minh \(DE.DM = D{N^2}\)
Do \(\Delta MEN\) nội tiếp nửa đường tròn \(\left( O \right)\) có cạnh MN là đường kính.
\(\Delta MEN\) vuông tại E (định lý) \( \Rightarrow NE \bot ME\) hay \(NE \bot MD\)
Xét \(\Delta MND\) vuông tại N (ND là tiếp tuyến của \(\left( O \right)\) tại N) có đường cao NE (\(NE \bot MD\))
\( \Rightarrow \) \(DE.DM = D{N^2}\) (hệ thức lượng trong tam giác vuông).
2) Từ O kẻ OI vuông góc với ME (\(I \in ME\)).
Chứng minh rẳng: 4 điểm O; I; D; N cùng thuộc một đường tròn.
Xét nửa đường tròn \(\left( O \right)\) có \(OI \bot ME\) (gt) \( \Rightarrow \angle OID = {90^o}\)
\( \Rightarrow \)\(\Delta OID\) vuông tại I \( \Rightarrow \Delta OID\) nội tiếp nửa đường tròn đường kính OD (định lý) (1)
Có ND là tiếp tuyến của \(\left( O \right)\) tại N \( \Rightarrow \angle OND = {90^o}\) (tính chất tiếp tuyến)
\( \Rightarrow \)\(\Delta OND\) vuông tại N \( \Rightarrow \) \(\Delta OND\) nội tiếp nửa đường tròn đường kính OD (định lý) (2)
Từ (1) và (2) \( \Rightarrow \) 4 điểm O; I; D; N cùng thuộc đường tròn đường kính OD.
3) Vẽ đường tròn đường kính OD, cắt nửa đường tròn tâm O tại điểm thứ hai là A. Chứng minh rằng: DA là tiếp tuyến của nửa đường tròn tâm O.
Do \(\Delta OAD\) nội tiếp nửa đường tròn đường kính OD
\( \Rightarrow \Delta OAD\) vuông tại A \( \Rightarrow OA \bot DA\) mà A thuộc nửa đường tròn tâm O (gt)
\( \Rightarrow \) DA là tiếp tuyến của nửa đường tròn tâm O (dhnb tiếp tuyến). (đpcm)
4) Chứng minh rằng: \(\angle DEA = \angle DAM\)
Ta có DA là tiếp tuyến của nửa đường tròn tâm O (cmt)
DN là tiếp tuyến của nửa đường tròn tâm O (gt)
\( \Rightarrow DA = DN\) (tính chất hai tiếp tuyến cắt nhau)
\( \Rightarrow D{A^2} = D{N^2} = DE.DM\;\;\left( {cmt} \right) \Rightarrow \frac{{DA}}{{DE}} = \frac{{DM}}{{DA}}\)
Xét \(\Delta ADM\) và \(\Delta EDA\) có: \(\angle D\) chung; \(\frac{{DA}}{{DE}} = \frac{{DM}}{{DA}}\;\;\left( {cmt} \right)\)
\( \Rightarrow \Delta ADM \sim \Delta EDA\;\;\left( {g - c - g} \right) \Rightarrow \angle DEA = \angle DAM\) (2 góc tương ứng) (đpcm).

