Cho điểm C thuộc nửa đường tròn đường kính AB. Kẻ tiếp tuyến Ax với nử

Câu hỏi
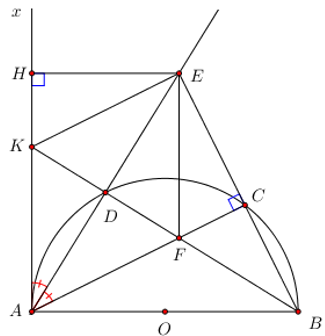
Nhận biếtCho điểm C thuộc nửa đường tròn đường kính AB. Kẻ tiếp tuyến Ax với nửa đường tròn đó (Ax nằm trên cùng nửa mặt phẳng có bờ là đường thẳng AB chứa nửa đường tròn). Tia phân giác của góc CAx cắt nửa đường tròn tại D. Kéo dài AD và BC cắt nhau tại E. Kẻ EH vuông góc với Ax tại H.
a) Chứng minh tứ giác AHEC nội tiếp.
b) Chứng minh \(\widehat {ABD} = \widehat {DBC}\).
c) Chứng minh tam giác ABE cân.
d) Tia BD cắt AC và Ax lần lượt tại F và K. Chứng minh AKEF là hình thoi.
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
a) Do \(\widehat {ACB}\) là góc nội tiếp chắn nửa đường tròn
\( \Rightarrow \widehat {ACB} = {90^0} \Rightarrow \widehat {ACE} = {90^0}\).
Xét tứ giác AHEC có \(\widehat {ACE} + \widehat {AHE} = {180^0}\)
\( \Rightarrow AHEC\) là tứ giác nội tiếp (Tứ giác có tổng hai góc đối bằng 1800)
b) Ta có \(\widehat {ABD} = \widehat {HAE}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và
dây cung cùng chắn cung AD).
Mà \(\widehat {HAE} = \widehat {CAE}\,\,\left( {gt} \right);\,\,\widehat {CAE} = \widehat {DBC}\) (hai góc nội tiếp cùng chắn cung CD).
\( \Rightarrow \widehat {ABD} = \widehat {DBC}\).
c) Ta có \(\widehat {ADB} = {90^0}\) (góc nội tiếp chắn nửa đường tròn) \( \Rightarrow BD \bot AE\).
\(\widehat {ABD} = \widehat {DBC}\,\,\left( {cmt} \right) \Rightarrow BD\) là phân giác của \(\widehat {ABE}\).
Tam giác \(ABE\) có BD là đường cao đồng thời là phân giác \( \Rightarrow \Delta ABE\) cân tại B.
d) Tam giác AKF có phân giác AD đồng thời là đường cao \( \Rightarrow \Delta AKF\) cân tại A \( \Rightarrow D\) là trung điểm của KF.
\(\Delta ABE\) cân tại B (cmt) \( \Rightarrow \) Đường cao BD đồng thời là trung tuyến\( \Rightarrow D\) là trung điểm của \(AE\).
\( \Rightarrow AKEF\) là hình bình hành (Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường).
Lại có \(AE\) là phân giác của \(\widehat {KAF}\) nên AKEF là hình thoi (Hình bình hành có một đường chéo là đường phân giác của một góc).

