Cho Delta ABC có hai trung tuyến BMCN vuông góc với nhau. Khi đó hệ thức nào sau đây đúng.

Câu hỏi
Nhận biếtCho \(\Delta ABC\) có hai trung tuyến \(BM,\,\,CN\) vuông góc với nhau. Khi đó, hệ thức nào sau đây đúng.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
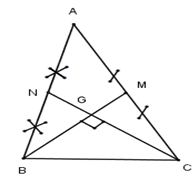
Ta có:
\(\eqalign{ & m_b^2 = {{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4} \cr & m_c^2 = {{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4} \cr} \)
\(BM \cap CN = \left\{ G \right\} \Rightarrow \) G là trọng tâm \(\Delta ABC \Rightarrow BG = {2 \over 3}{m_b};\,\,\,CG = {2 \over 3}{m_c}\)
\(BM \bot CN \Leftrightarrow \Delta BGC\) vuông tại G.
\(\eqalign{ & \Leftrightarrow B{G^2} + C{G^2} = B{C^2} \cr & \Leftrightarrow {\left( {{2 \over 3}{m_b}} \right)^2} + {\left( {{2 \over 3}{m_c}} \right)^2} = {a^2} \cr & \Leftrightarrow {4 \over 9}\left( {{{{a^2} + {c^2}} \over 2} - {{{b^2}} \over 4}} \right) + {4 \over 9}\left( {{{{a^2} + {b^2}} \over 2} - {{{c^2}} \over 4}} \right) = {a^2} \cr & \Leftrightarrow 2\left( {{a^2} + {c^2}} \right) - {b^2} + 2\left( {{a^2} + {b^2}} \right) - {c^2} = 9{a^2} \cr & \Leftrightarrow 2{a^2} + 2{c^2} - {b^2} + 2{a^2} + 2{b^2} - {c^2} = 9{a^2} \cr & \Leftrightarrow {b^2} + {c^2} = 5{a^2} \cr} \)
Chọn D
