Cho các số thực xy thay đổi thỏa mãn x + y = 2.Tìm giá trị nhỏ nhất của biểu thức : P = (x4 + 1)(y4
Câu hỏi
Nhận biếtCho các số thực x,y thay đổi thỏa mãn x + y = 2.Tìm giá trị nhỏ nhất của biểu thức : P = (x4 + 1)(y4 + 1) + 2013
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Ta có P = (x4 + 1)(y4 + 1) + 2013
= x4y4 + x4 + y4 + 1 +2013 = x4y4 + (x2 + y2)2 – 2x2y2 + 1 + 2013
= (x2y2 – 1)2 + (x2 + y2)2 + 2103 = (x2y2 – 1)2 + (4 – 2xy)2 + 2013
= (x2y2 – 1)2 + 16 – 16xy + 4x2y2 + 2103
= (x2y2 – 1)2 + 4(xy – 1)2 – 8xy + 2025 ≥ (x2y2 - 1) + 4(xy – 1)2 – 2(x + y)2 + 205
= (x2y2 – 1)2 + 4(xy – 1)2 + 2017 ≥ 2017
Vậy giá trị nhỏ nhất của P là 2017 khi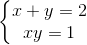 
⇔ x = y =1
