Cho các số thực dương x y thỏa mãn (x + y – 1)2 = xy Tìm giá trị nhỏ nhất của biểu thức P = <

Câu hỏi
Nhận biếtCho các số thực dương x, y thỏa mãn (x + y – 1)2 = xy
Tìm giá trị nhỏ nhất của biểu thức
P = 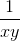 +
+ 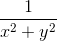 +
+ 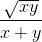
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta có (x + y – 1)2 = xy => [(x – 1) + (y – 1) + 1]2 = xy
=>(x – 1)2 + (y – 1)2 + 2(x – 1)(y – 1) + 2(x – 1) + 2(y – 1) + 1 = xy
=>(x – 1)2 + (y – 1)2 = 1 – xy
=> 1 – xy ≥ 0 => xy ≤ 1
=> (x – 1)2 + (y – 1)2 ≤ 1; xy ≤ 1; x > 0; y > 0 (gt)
=>  ≥ 1 ; x + y ≤ 2 =>
≥ 1 ; x + y ≤ 2 =>  ≥ 1;
≥ 1;  ≥
≥  (*)
(*)
Mà P =  +
+ 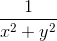 +
+  +
+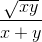
Ap dụng bất đẳng thức phụ 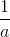 +
+  ≥
≥  và bđt Cô si a + b ≥ 2√ab ta có
và bđt Cô si a + b ≥ 2√ab ta có
P ≥  + 2
+ 2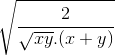 (**)
(**)
Từ (*) và (*) => P ≥  +
+  + = 2. Dấu « = » xảy ra khi x = y =1
+ = 2. Dấu « = » xảy ra khi x = y =1

