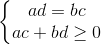[LỜI GIẢI] Cho các số thực a, b, c, d. Chứng minh:   - Tự Học 365
LUYỆN TẬP TRẮC NGHIỆM 50000+ CÂU HỎI

DÀNH CHO MỌI LỚP 6 ĐẾN 12

TRUY CẬP NGAY
XEM CHI TIẾT

Cho các số thực a, b, c, d. Chứng minh:  

Câu hỏi

Nhận biết

Cho các số thực a, b, c, d. Chứng minh:

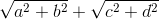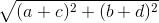
\sqrt{a^{2}+b^{2}}+\sqrt{c^{2}+d^{2} ≥ \sqrt{(a+c)^{2}+(b+d)^{2}}

Đẳng thức xảy ra ki nào?


Đáp án đúng: A

Lời giải của Tự Học 365

Giải chi tiết:

           ≥ 

<=>   

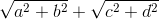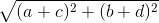
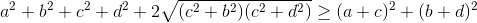
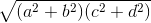<=>    ≥ ac + bd    (1).

Nếu ac + bd < 0 thì bất đẳng thức (1) hiển nhiên đúng.

Nếu ac + bd ≤ 0 thì bất đẳng thức (1) tương đương với 

         (a2 + b2)(c2 + d2) ≥ (ac + bd)2      <=> (ad – bc)2 ≥ 0 (đúng)

Vậy bất đẳng thức đầu luôn đúng.

Dấu đẳng thức xảy ra khi  

Ý kiến của bạn

Luyện tập

Câu hỏi liên quan

  •  (1 điểm) Vẽ đồ thị của hàm số y = -2x<sup>2</sup>.

     (1 điểm) Vẽ đồ thị của hàm số y = -2x2.

    Chi tiết
  • Diện tích mặt cầu có bán kính bằng 2 cm là:

    Diện tích mặt cầu có bán kính bằng 2 cm là:

    Chi tiết
  • Hàm số nào sau đây không phải là hàm số bậc nhất?

    Hàm số nào sau đây không phải là hàm số bậc nhất?

    Chi tiết
  • Hàm số nào sau đây nghịch biến trên R?

    Hàm số nào sau đây nghịch biến trên R?

    Chi tiết
  • (1 điểm) Giải phương trình:  2x<sup>2</sup> + x – 15 = 0

    (1 điểm) Giải phương trình:  2x2 + x – 15 = 0

    Chi tiết
  • Phương trình nào sau đây có đúng hai nghiệm phân biệt:

    Phương trình nào sau đây có đúng hai nghiệm phân biệt:

    Chi tiết
  •  Phương trình 3x<sup>2</sup> – 5x – 2015 có tổng hai nghiệm

     Phương trình 3x2 – 5x – 2015 có tổng hai nghiệm là:

    Chi tiết
  • Khối nón có chiều cao bằng 12 cm, đường sinh bằng 15 cm thì

    Khối nón có chiều cao bằng 12 cm, đường sinh bằng 15 cm thì có thể tích là:

    Chi tiết

  • Hàm số nào đồng biến trên R:

    Chi tiết
  • Cho đường tròn (O; 25 cm) và dây AB = 40 cm. Khi đó khoảng c

    Cho đường tròn (O; 25 cm) và dây AB = 40 cm. Khi đó khoảng cách từ tâm O đến dây AB là:

    Chi tiết