Cho a b là các số dương thoả mãn ab = 1. Tìm giá trị nhỏ nhất của biểu thức: A = (a + b + 1)(a2 + b2
Câu hỏi
Nhận biếtCho a, b là các số dương thoả mãn ab = 1. Tìm giá trị nhỏ nhất của biểu thức: A = (a + b + 1)(a2 + b2) +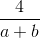 
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: a2 + b2 > 2ab = 1 (vì ab = 1)
A = (a + b + 1)(a2 + b2) +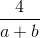 
> 2(a + b + 1) +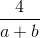
= 2 + (a + b + 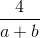) + (a + b) > 2 + 4 + 2 = 8.
(a + b + >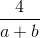 
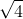và a + b > 2
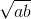vì áp dụng BĐT Côsi cho 2 số dương)
Dấu “=” khi và chỉ khi a = b = 
.
Vậy minA = 8.
