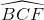Cho ∆ABC có 3 góc nhọn. Kẻ các đường cao AD; BE; CF. Chứng mih rằng: AD.BE.CF = AB.AC.BC.sinA.sinB.

Câu hỏi
Nhận biếtCho ∆ABC có 3 góc nhọn. Kẻ các đường cao AD; BE; CF. Chứng mih rằng:
AD.BE.CF = AB.AC.BC.sinA.sinB.sinC = AB.AC.BC.cos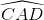 .cos
.cos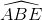 .cos
.cos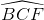
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:

∆ACD vuông tại D: 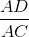 = sinC = cos
= sinC = cos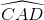 (1)
(1)
∆ABE vuông tại E: 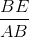 = sinA = cos
= sinA = cos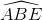 (2)
(2)
∆BCF vuông tại F: 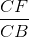 = sinB = cos
= sinB = cos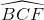 (3)
(3)
Từ (1), (2), (3) suy ra: 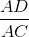 .
.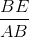 .
.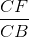
= sinA.sinB.sinC = cos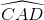 .cos
.cos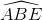 .cos
.cos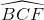
Suy ra AD.BE.CF = AB.AC.BC.sinA.sinB.sinC
= AB.AC.BC.cos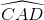 .cos
.cos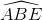 .cos
.cos