Cầu Vàm Cống bắc ngang qua sông Hậu nối liền hai tỉnh Cần Thơ và Đồng
Câu hỏi
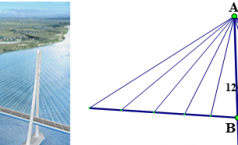
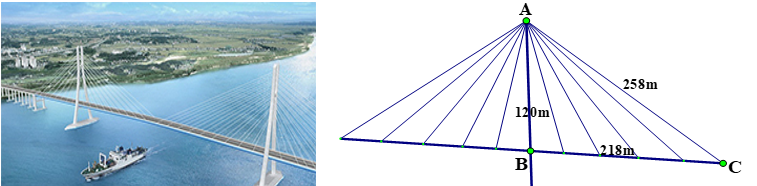
Nhận biếtCầu Vàm Cống bắc ngang qua sông Hậu nối liền hai tỉnh Cần Thơ và Đồng Tháp thiết kế theo kiểu dây giăng như hình vẽ. Chiều cao từ sàn cầu đến đỉnh trụ đỡ AB =120m, dây giăng
AC =258m, chiều dài sàn cầu từ B đến C là 218m. Hỏi góc nghiêng của sàn cầu BC so với mặt nằm ngang là bao nhiêu độ? (Giả thiết xem như trụ đỡ AB thẳng đứng).
Đáp án đúng:
Lời giải của Tự Học 365
Giải chi tiết:
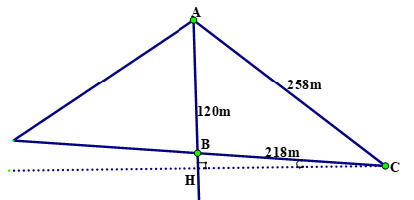
Gọi H là hình chiếu vuông góc của C lên trụ đỡ AB. Đặt: BH = x \(\left( x>0,m \right)\) Tam giác AHC vuông tại H, áp dụng định lý Pitago, ta có:
\(H{{C}^{2}}=A{{C}^{2}}-A{{H}^{2}}=A{{C}^{2}}-{{\left( AB+BH \right)}^{2}}={{258}^{2}}-{{\left( 120+x \right)}^{2}}\) (1)
Tam giác BHC vuông tại H, áp dụng định lý Pitago, ta có:
\(H{{C}^{2}}=B{{C}^{2}}-B{{H}^{2}}={{218}^{2}}-{{x}^{2}}\) (2)
Từ (1) và (2) suy ra:
\(\begin{array}{l}{258^2} - {\left( {120 + x} \right)^2} = {218^2} - {x^2}\\ \Leftrightarrow {258^2} - \left( {{{120}^2} + 240x + {x^2}} \right) = {218^2} - {x^2}\\ \Leftrightarrow {258^2} - {120^2} - {218^2} = 240x\\ \Leftrightarrow x = \frac{{58}}{3}\end{array}\)
Xét tam giác vuông BHC ta có:
\(\sin BCH=\frac{BH}{BC}=\frac{58}{3.218}=\frac{29}{327}\Rightarrow \) góc \(BHC={{5}^{0}}5'16''\)
Vậy góc nghiêng BC so với mặt nằm ngang là \({{5}^{0}}5'16''\)


