Bát giác đều ABCDEFGH nội tiếp đường tròn bán kính bằng 1. Tính độ dài cạnh AB của bát giác

Câu hỏi
Nhận biếtBát giác đều ABCDEFGH nội tiếp đường tròn bán kính bằng 1. Tính độ dài cạnh AB của bát giác
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
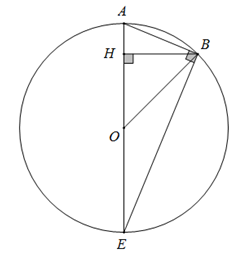
Vì ABCDEFGH là bát giác đều nên góc AOB bằng 45o và AE là đường kính của đường tròn (O) ngoại tiếp bát giác.
Vẽ BH ⊥ AO tại H thì tam giác BHO vuông cân tại H. Suy ra
\(\begin{array}{l}BH = OH = \frac{{OB}}{{\sqrt 2 }} = \frac{1}{{\sqrt 2 }}\\AH = AO - OH = 1 - \frac{1}{{\sqrt 2 }}\\AE = 2AO = 2\end{array}\)
Vì AE là đường kính của (O) nên ∆ ABE vuông tại B, áp dụng hệ thức lượng trong tam giác vuông ta có
\(A{B^2} = AH.AE = \left( {1 - \frac{1}{{\sqrt 2 }}} \right).2 = 2 - \sqrt 2 \)
\( \Rightarrow AB = \sqrt {2 - \sqrt 2 } \)
Chọn C

