Bán kính đường tròn ngoại tiếp ∆BHC bằng R.
Câu hỏi
Nhận biếtBán kính đường tròn ngoại tiếp ∆BHC bằng R.
Đáp án đúng: B
Lời giải của Tự Học 365
Cách giải nhanh bài tập này
Gọi K là giao điểm của AD và đường tròn (O) (K ≠ A)
Vẽ OI ⊥ BC tại I, gọi O’ là điểm đối xứng của O qua I
Ta có I là trung điểm của BC
Do vậy BOCO’ là hình bình hành
=> O’B = OC = R; O’C = OB = R
Ta có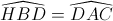 
(cùng phụ với 
)
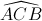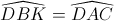(hai góc nội tiếp cùng chắn cung CK)
Do đó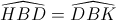 
∆BHK có BD vừa là đường cao(BD⊥HK) vừa là đường phân giác ()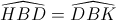
=> ∆BHK cân tại B=> BC là đường trung trực của HK
Nên H, K đối xứng qua BC
Mà O’, O đối xứng qua BC
Do đó O’H = OK = R (Tính chất đối xứng trục)
Ta có O’B = O’H = O’C = R
Vậy bán kính đường tròn ngoại tiếp tam giác BHC bằng R.
