Ba người đi xe đạp xuất phát từ A đi về B. Người thứ nhất đi với vận t

Câu hỏi
Nhận biếtBa người đi xe đạp xuất phát từ A đi về B. Người thứ nhất đi với vận tốc v1 = 8km/h. Sau đó 15 phút người thứ hai xuất phát với vận tốc v2 = 12km/h. Người thứ ba đi sau người thứ hai 30 phút. Sau khi gặp người thứ nhất, người thứ ba đi thêm 30 phút nữa thì sẽ ở cách đều người thứ nhất và người thứ hai. Tính vận tốc của người thứ ba.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Khi người thứ ba xuất phát thì:
+ Người thứ nhất đã đi được: l1 = v1.to1 = 8  = 6 km
= 6 km
+ Người thứ hai đã đi được: l2 = v2.to2 = 12.0,5 = 6 km
Gọi t1 là thời gian người thứ 3 đi đến gặp người thứ nhất:
v3.t1 = l1 + v1t1 => t1 = 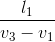 =
= 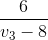 (1)
(1)
Sau t2 = t1 + 0,5 thì:
+ quãng đường người thứ nhất đi được: S1 = l1 + v1t2 = 6 + 8( t1 + 0,5 )
+ quãng đường người thứ hai đi được: S2 = l2 + v2t2 = 6 + 12( t1 + 0,5 )
+ quãng đường người thứ ba đi được: S3 = v3t2 = v3( t1 + 0,5 )
Theo đề: S3 – S1 = S2 – S3
<=> S1 + S2 =2S3
<=> 6 + 8( t1 + 0,5 ) + 6 + 12( t1 + 0,5 ) = 2[v3( t1 + 0,5 )]
<=> 12 = ( t1 + 0,5 )( 2v3 – 20 ) (2)
Thay (1) vào (2) ta được: v32 -18v3 + 56 = 0
Giải ra: v3 = 4 km/h ( loại vì v3 < v1 ) hoặc v3 = 14 km/h ( nhận )








