a) Viết phương trình parabol (P): y = ax^2 + bx + c biết (P) đi qua điểm M( - 2; - 3)và nhận điể

Câu hỏi
Nhận biếta) Viết phương trình parabol (P): \(y = a{x^2} + bx + c\) biết (P) đi qua điểm \(M( - 2; - 3)\)và nhận điểm \(I( - 1; - 4)\) làm đỉnh.
b) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} + 2x - 3\)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
a) Viết phương trình parabol (P): \(y = a{x^2} + bx + c\) biết (P) đi qua điểm \(M( - 2; - 3)\)và nhận điểm \(I( - 1; - 4)\) làm đỉnh.
Theo đề bài ta có: \(\left\{ \begin{array}{l}a \ne 0\\4a - 2b + c = - 3\\\frac{{ - b}}{{2a}} = - 1\\a - b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\4a - 2b + c = - 3\\2a - b = 0\\a - b + c = - 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a \ne 0\\a = 1\\b = 2\\c = - 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 1\\b = 2\\c = - 3\end{array} \right..\)
Vậy phương trình parabol (P): \(y = {x^2} + 2x - 3\)
b) Lập bảng biến thiên và vẽ đồ thị hàm số \(y = {x^2} + 2x - 3\)
+ Tập xác định \(D = R\).
+ Bảng biến thiên:
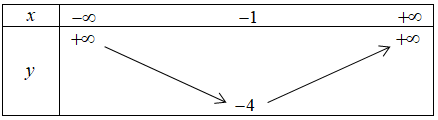
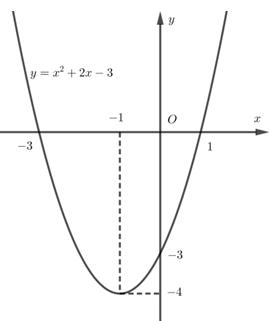
+ Vẽ đồ thị hàm số
+ Đỉnh \(I\left( { - 1; - 4} \right)\)
+ Trục đối xứng \(x = - 1\)
+ Giao với trục tung \(A\left( {0; - 3} \right)\)
+ Giao với trục hoành tại \(B\left( {1;0} \right);\,\,B'\left( { - 3;0} \right)\).