a) Viết phương trình đường thẳng (d) song song với đường thẳng y

Câu hỏi
Nhận biếta) Viết phương trình đường thẳng (d) song song với đường thẳng y = 3x + 1 và cắt trục tung tại điểm có tung độ bằng 4.
b) Vẽ đồ thị hàm số y = 3x + 4 (d) và \(y=- \frac{{{x}^{2}}}{2} \) (P) trên cùng một mặt phẳng tọa độ. Tìm tọa độ các giao điểm của hai đồ thị ấy bằng phép tính.
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Giả sử phương trình đường thẳng (d) có dạng: y = ax + b (1) với \(a\ne 0\). Do (d) song song với đường thẳng y = 3x + 1 nên suy ra: \(\left\{ \begin{align} a=3 \\ b\ne 1 \\ \end{align} \right.\) Mặt khác, (d) cắt trục tung tại điểm có tọa độ x = 0; y = 4. Thế x =0, y = 4, a = 3 vào phương trình (1), ta được:
\(4=3.0+b\Leftrightarrow b=4\) (thỏa mãn \(b\ne 1\))
Vậy phương trình đường thẳng (d) cần tìm là: y = 3x + 4
b) 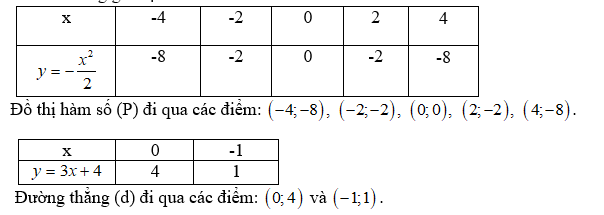
Đồ thị. 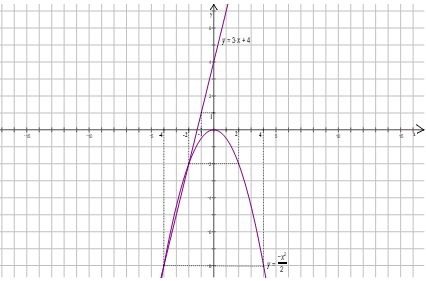
Phương trình hoành độ giao điểm của (P) và (d) là:
\(\begin{array}{l} - \frac{1}{2}{x^2} = 3x + 4 \Leftrightarrow - {x^2} = 6x + 8 \Leftrightarrow {x^2} + 6x + 8 = 0 \Leftrightarrow {x^2} + 4x + 2x + 8 = 0\\ \Leftrightarrow x\left( {x + 4} \right) + 2\left( {x + 4} \right) = 0 \Leftrightarrow \left( {x + 4} \right).\left( {x + 2} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x + 4 = 0\\x + 2 = 0\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = - 4\\x = - 2\end{array} \right.\end{array}\)
Với x = -2 thế vào phương trình (d): \(y=3x+4\), ta được: y = -2
Với x = -4 thế vào phương trình (d): \(y=3x+4\), ta được: y = -8
Vậy: (d) cắt (P) tại hai điểm \(\left( -2;-2 \right)\) và \(\left( -4;-8 \right)\).

