a) Trong mặt phẳng tọa độ Oxy cho parabol (P): y=x^2. Vẽ đồ thị hàm số (P). b) Cho phương t

Câu hỏi
Nhận biếta) Trong mặt phẳng tọa độ Oxy, cho parabol (P): \(y={{x}^{2}}.\) Vẽ đồ thị hàm số (P).
b) Cho phương trình: \({{x}^{2}}-(m-1)x-m=0\). Xác định các giá trị của m để phương trình có 2 nghiệm phân biệt \({{x}_{1}},\ \ {{x}_{2}}\) thỏa mãn: \({{x}_{1}}(3-{{x}_{2}})+20\ge 3(3-{{x}_{2}}).\)
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
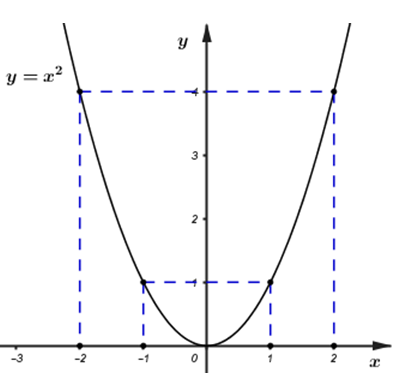
a) Trong mặt phẳng tọa độ Oxy, cho parabol (P): \(y={{x}^{2}}.\) Vẽ đồ thị hàm số (P).
Ta có bảng giá trị:

Như vậy đồ thị hàm số \(\left( P \right):\ y={{x}^{2}}\) đi qua các điểm \(\left( -2;\ 4 \right),\ \left( -1;\ 1 \right),\ \left( 0;\ 0 \right),\ \left( 1;\ 1 \right),\ \left( 2;\ 4 \right).\)
b) Cho phương trình: \({{x}^{2}}-(m-1)x-m=0\). Xác định các giá trị của m để phương trình có 2 nghiệm phân biệt \({{x}_{1}},\ \ {{x}_{2}}\) thỏa mãn: \({{x}_{1}}(3-{{x}_{2}})+20\ge 3(3-{{x}_{2}}).\)
Để phương trình có 2 nghiệm phân biệt thì: \(\Delta >0\Leftrightarrow {{(m-1)}^{2}}+4m>0\Leftrightarrow {{(m+1)}^{2}}>0\Leftrightarrow m\ne -1.\)
Áp dụng định lý Vi-et ta có: \(\left\{ \begin{align} & {{x}_{1}}+{{x}_{2}}=m-1 \\ & {{x}_{1}}{{x}_{2}}=-m \\ \end{align} \right.\)
Theo đề bài ta có : \({{x}_{1}}(3-{{x}_{2}})+20\ge 3(3-{{x}_{2}})\)
\(\begin{align} & \Leftrightarrow 3{{x}_{1}}-{{x}_{1}}{{x}_{2}}+20\ge 9-3{{x}_{2}} \\ & \Leftrightarrow 3({{x}_{1}}+{{x}_{2}})-{{x}_{1}}{{x}_{2}}\ge -11 \\ & \Leftrightarrow 3\left( m-1 \right)+m\ge -11 \\ & \Leftrightarrow 3m-3+m+11\ge 0 \\ & \Leftrightarrow 4m+8\ge 0 \\ & \Leftrightarrow m\ge -2. \\ \end{align}\)
Kết hợp điều kiện, ta có : \(\left\{ \begin{align} & m\ge -2 \\ & m\ne -1 \\ \end{align} \right..\)
Vậy \(m\ge -2,\ \ m\ne 1\) thỏa mãn điều kiện bài toán.
Chọn D

