a) Trong mặt phẳng tọa độ ( Oxy ) cho parabol ( P ):,,y = - 2x^2. Vẽ
Câu hỏi
Nhận biếta) Trong mặt phẳng tọa độ \(\left( {Oxy} \right)\) cho parabol \(\left( P \right):\,\,y = - 2{x^2}.\) Vẽ \(\left( P \right).\)
b) Tìm \(m\) để đường thẳng \(y = \left( {5m - 2} \right)x + 2019\) song song với đường thẳng \(y = x + 3.\)
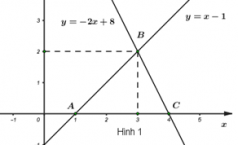
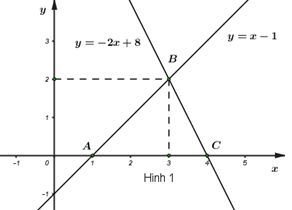
c) Hai đường thẳng \(y = x - 1\) và \(y = - 2x + 8\) cắt nhau tại điểm \(B\) và lần lượt cắt trục \(Ox\) tại điểm \(A,\,\,C\) (hình 1). Xác định tọa độ các điểm \(A,\,\,B,\,\,C\) và tính diện tích tam giác \(ABC.\)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
a) Trong mặt phẳng tọa độ \(\left( {Oxy} \right)\) cho parabol \(\left( P \right):\,\,y = - 2{x^2}.\) Vẽ \(\left( P \right).\)
Ta có bảng giá trị:

Vậy đồ thị hàm số \(\left( P \right):\,\,\,y = - 2{x^2}\) là đường cong đi qua các điểm \(\left( { - 2; - 8} \right),\,\,\left( { - 1; - 2} \right),\,\,\left( {0;\,\,0} \right),\,\,\left( {1;\, - 2} \right),\,\,\left( {2;\, - 8} \right).\)
Đồ thị hàm số \(\left( P \right):\,\,\,y = - 2{x^2}\)
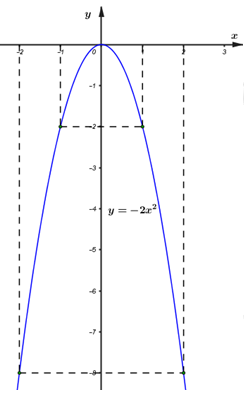
b) Tìm \(m\) để đường thẳng \(y = \left( {5m - 2} \right)x + 2019\) song song với đường thẳng \(y = x + 3.\)
Đường thẳng \(y = \left( {5m - 2} \right)x + 2019\) song song với đường thẳng \(y = x + 3\)
\( \Leftrightarrow \left\{ \begin{array}{l}5m - 2 = 1\\2019 \ne 3\,\,\left( {luon\,\,dung} \right)\end{array} \right. \Leftrightarrow 5m = 1 + 2 \Leftrightarrow m = \frac{3}{5}.\)
Vậy \(m = \frac{3}{5}\) thỏa mãn bài toán.
c) Hai đường thẳng \(y = x - 1\) và \(y = - 2x + 8\) cắt nhau tại điểm \(B\) và lần lượt cắt trục \(Ox\) tại điểm \(A,\,\,C\) (hình 1). Xác định tọa độ các điểm \(A,\,\,B,\,\,C\) và tính diện tích tam giác \(ABC.\)
Dựa vào Hình 1 ta thấy tọa độ các điểm \(A,\,\,B,\,\,C\) là: \(A\left( {1;\,\,0} \right),\,\,\,B\left( {3;\,\,2} \right),\,\,\,C\left( {4;\,\,0} \right).\)
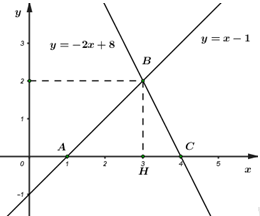
Gọi \(H\) là hình chiếu vuông góc của \(B\) trên \(AC,\,\) ta có: \({S_{ABC}} = \frac{1}{2}BH.AC.\)
Ta có: \(\left\{ \begin{array}{l}BH = {y_B} = 2\\AC = {x_C} - {x_A} = 4 - 1 = 3\end{array} \right. \Rightarrow {S_{ABC}} = \frac{1}{2}BH.AC = \frac{1}{2}.2.3 = 3\) (đvdt).
Chọn A.


